Ache o volume do sólido de revolução gerado ao girar em torno do eixo a região limitada pela curva , pelo eixo e pela reta .

O exercício pede o volume do sólido obtido pela revolução da região limitada pela curva e as retas e em torno do eixo . Um esboço dessa região é dado a seguir:

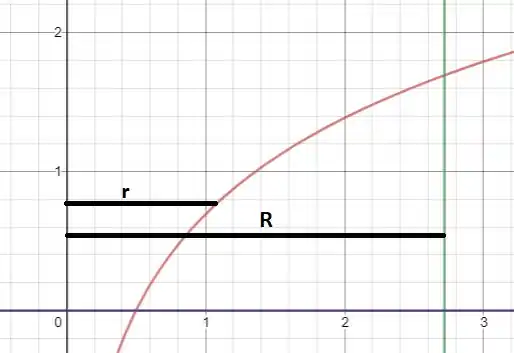
Como o sólido é girado em torno do eixo , a integração será feita na variável . Neste caso, o volume do sólido de revolução é dado por

onde e são os “raios” ( como função de ) das seções circulares que são integradas para dar o volume. Neste caso, . Para achar , precisamos exprimir em função de na equação :

Já para os limites de integração, enquanto é obtido pela interseção da reta com a curva :

Tomando nos dois lados:

Portanto, . Assim, o volume será