Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.Revisão - Ex. 102

A região no primeiro quadrante, limitada pela curva y = 5 - x x + 1 2 , pelo eixo x e pelo eixo y gira em torno do eixo x . Ache o volume do sólido gerado.

Passo 1

O exercício pede o volume do sólido obtido pela revolução da região limitada pela curva y = ln ⁡ 2 x e as retas x = e e y = 0 em torno do eixo y . Um esboço dessa região é dado a seguir:

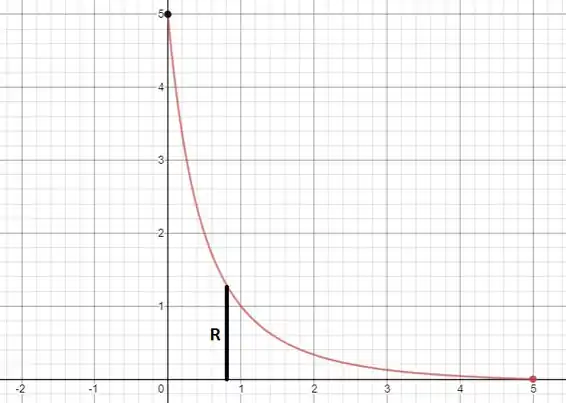
As interseções com os eixos são ( 0 ,   5 ) e ( 5 ,   0 ) . Como a região é rotacionada em torno do eixo x , o volume será

V = ∫ a b π   R 2   d x

Os limites de integração serão a = 0 e b = 5 , enquanto R = y = 5 - x x + 1 2 . Assim, o volume será

V = π ∫ 0 5 5 - x 2 x + 1 4   d x

Passo 2

Para calcular essa integral, temos que fazer a mudança t = x + 1 ⇒ d x = d t com x = t - 1 . Assim,

V = π ∫ 1 6 5 - t + 1 2 t 4   d t = π ∫ 1 6 6 - t 2 t 4   d t

Note que os limites de integração também devem ser alterados!

Podemos escrever então,

V = π ∫ 1 6 36 - 12 t + t 2 t 4   d t = π ∫ 1 6 36 t - 4 - 12 t - 3 + t - 2   d t

Passo 3

Fazendo a integração:

V = π   - 12 t 3 + 6 t 2 - 1 t 1 6 = π - 12 216 + 6 36 - 1 6 + 12 - 6 + 1

Logo,

V = π - 1 18 + 1 6 - 1 6 + 7 = 125 π 18

Resposta

125 π 18

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule as integrais nos Exercícios 1-34.9. ∫ 0 π 3 2 s e c 2 xd x
Calcule as integrais nos Exercícios 1-34.3. ∫ 0 2 x ( x - 3 ) d x
Calcule as integrais nos Exercícios 1-34.21. ∫ 2 1 u 7 2 - 1 u 5 d u
Calcule as integrais nos Exercícios 1-34.23. ∫ 1 2 ( s 2 + s ) s ² d s ²
Calcule as integrais nos Exercícios 1-34.17. ∫ 0 π 8 s e n2 x d x