Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.2 - Ex. 45
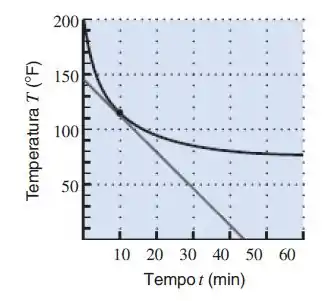
De acordo com a Lei do Resfriamento de Newton, a taxa de variação da temperatura de um objeto é proporcional à diferença entre a sua temperatura e a do meio ambiente. A figura a seguir mostra o gráfico da temperatura (em graus Fahernheit) versus o tempo (em minutos) para uma xícara de café inicialmente a F, deixada para esfriar em uma sala com uma temperatura constante de F.
- Estime e quando min.
- A Lei do Resfriamento de Newton pode ser expressa por
onde é a constante de proporcionalidade e , a temperatura do meio ambiente (constante, por hipótese). Use os resultados de (a) para estimar o valor de .
Passo 1
- Analisando o gráfico, nós vemos que quando a temperatura é igual a .
- Para estimar o valor de é simples, vamos substituir os valores que achamos em:
Já para estimar vamos achar a inclinação nesse ponto usando:
Onde e são pontos da reta tangente, vamos substituir então:
Passo 2
E temos que é a temperatura inicialmente a F, vamos lá então:
Resposta
- e
Exercícios de Livros Relacionados
Nos exercícios de 1 a 24, derive a função dada, aplicando os teoremas desta secção. f x = 7 x - 5
Nos exercícios de 1 a 24, derive a função dada, aplicando os teoremas desta secção.5. f x = x 3 - 3 x 2 + 5 x - 2
Nos exercícios de 1 a 24, derive a função dada, aplicando os teoremas desta secção.4. f x = 4 x 2 + x + 1
Nos exercícios de 1 a 24, derive a função dada, aplicando os teoremas desta secção.9. F x = 1 4 t 4 - 1 2 t 2
Nos exercícios de 1 a 24, derive a função dada, aplicando os teoremas desta secção.13. F x = x 2 + 3 x + 1 x 2