Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.2 - Ex. 44
A figura abaixo mostra a curva velocidade versus tempo para um foguete no espaço extraterrestre, onde a única força atuando sobre o foguete é a de seus motores. Pode ser mostrado que a massa do foguete no instante (em segundos) satisfaz a equação
onde é o empuxo (em libras) dos motores do foguete e é a velocidade (em pés/s) do foguete. O empuxo do primeiro estágio do foguete Saturno é de libras. Use esse valor de e o segmento de reta na figura para estimar a massa do foguete no instante s.
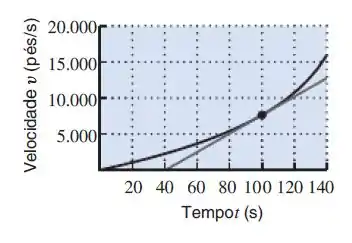
Passo 1
Para estimar a massa do foguete no instante s vamos usar a fórmula:
Precisamos achar , que é a inclinação em , vamos achar a inclinação nesse ponto usando:
Onde e são pontos da reta tangente, vamos substituir então:
Passo 2
Agora é só substituir esse valor na equação:
Assim, a massa do foguete no instante s é de .