Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 53
Use a definição de derivada para encontrar . A seguir, trace , e em uma mesma tela e verifique se suas respostas são razoáveis.
Passo 1
Opa, vamos fazer essa questão! O enunciado nos dá:
Pede pra a gente calcular pela definição de derivada, traçar os gráficos de e e no final a gente precisa analisar esses gráficos pra ver se eles fazem sentido!
Vamos relembrar a definição de derivada:
Aqui não tem mistério, temos que substituir e calcular. O único ponto de atenção é que, como não podemos calcular direto, se não teremos uma indeterminação! Então vamos ter que dar aquela manipulada no limite pra fugir disso.
Para calcular é só a gente usar a fórmula acima de novo, só que agora em cima de , beleza?!
Passo 2
Vamos calcular a derivada primeira. Substituindo nossa função na definição de derivada:
Abrindo:
Isolando o :
Depois que a gente cortar o já podemos calcular o limite:
Passo 3
Vamos aplicar a definição de derivada em e encontrar , teremos que:
Substituindo:
Passo 4
Agora plotamos os gráficos:
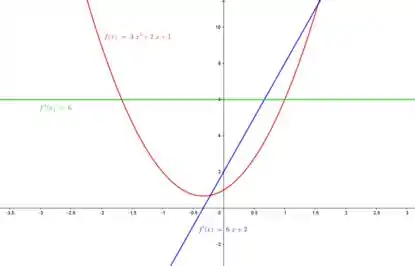
Podemos comparar alguns pontos chaves que poderíamos esperar da função e suas derivadas primeira e segunda com as curvas ai de cima!
Primeiro é decrescente, portanto a inclinação de suas tangentes vão ser negativas. Depois ela chega a um ponto mínimo onde a tangente será horizontal, logo e em seguida ela passa a ser crescente, logo com inclinação da reta tangente positiva!
Poderíamos esperar uma reta de que primeiro tem valores negativos, corta e segue com valores positivos! E é o que temos!
Agora, se é uma reta, então ela tem inclinação constante, certo?! Ou seja, pra todo teremos o mesmo valor de em . Esse é exatamente o resultado que a curva acima mostra!
Então, são soluções razoáveis (e corretas)!