Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.5 - Ex. 21
Administrando um Recurso Renovável. Suponha que a população de determinada espécie de peixe (por exemplor, atum ou linguado gigante) em certa área do oceano é descrita pela equação logística
Embora seja desejável utilizar essa fonte de alimento, é claro, instuitivamente, que, se forem pescados peixes demais, a população de peixes pode ser reduzida a um nível abaixo de utilizade, podemos até ser levada à extinção. Os problemas 20 e 21 exploram algumas das questões envolvidas na formulação de uma estratégia racional para administrar a pesca.
21. Nesse problema vamos supor que os peixes são pegos a uma taxa constante independente do tamanho da população. Então satifaz
A hipótese de que a taxa de pesca é constante pode ser razoável quando é muito grande, mas torna-se menos razoável quando é pequeno.
(a) Se , mostre que a Eq. Tem dois pontos de equilíbrio e com ; determine esses pontos.
(b) Mostre que é instável e que é assintoticamente estável.
(c) Analisando o gráfico em função de , mostre que, se a população inicial , então quando ; mas, se , então diminuiu quando aumenta. Note que não é um ponto de equilíbrio, de modo que, se , a população será extinta em um tempo finito.
(d) Se , mostre que diminui até zero quando aumenta, independente do valor de .
(e) Se , mostre que existe um único ponto de equilíbrio e que esse ponto é semiestável (veja o problema 7). Logo, a produção máxima sustentável é , correspondendo ao valor de equilíbrio . Note que tem o mesmo valor que no problema 20(d). A pesca é considerada superexploratada se se reduzir a um nível abaixo de .
Passo 1
Meus deus, que questão gigante. Nem quero mais faze-la, mas fazer o que...
Neste primeiro passo ficamos só com a parte que nos assustamos com o tamanho da questão, mas vamos já indicar que ela é trabalhosa, não difícil.
Passo 2
(a) Primeiro vamos analisar de forma mais geral os pontos críticos e depois começar a fazer as considerações solicitadas.
Os pontos críticos (equilíbrio) são aqueles onde a derivada da nossa função é nula, ou seja
Resolvendo, ficamos com
Uma equação de segundo grau. Lembra de báskara?
Onde nossa raiz só tem sentido real para
Ou seja, teremos doi pontos de equilíbri se, e somente se
Passo 3
(b) Para sabermos sobre a estabilidade do nossos pontos, vamos derivar mais uma vez nossa função e analisar o sinal da mesma próximo aos pontos.
Da nossa função, temos que
Para
E para
Assim para nosso ponto é assintoticamente instavel. E para temos um ponto que é assintoticamente estável.
Passo 4
(c) Olhando para o gráfico de por onde temos que em , por se tratar de um ponto instável, temos que quando . Já se , temos que quando t aumenta, temos que diminui
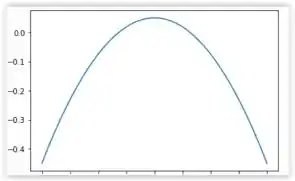
Passo 5
(d) Se , temos que não há ponto de instabilidade e
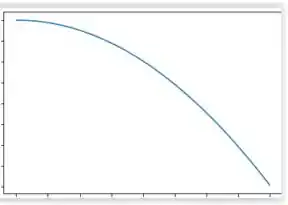
Quando aumenta, temos que diminui drasticamente.
Passo 6
(e) Quando , então
E e não como sugerido
Resposta
Ei, a resposta está no passo a passo :)