Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 2.5 - Ex. 25
Ponto de Bifurcação. Para uma equação da forma,
Em que é um parâmetro real, os pontos críticos (soluções de equilíbrio) dependem, em geral, do valor de . Quando aumenta ou diminui constantemente, acontece, muitas vezes, que, para determinado valor de , chamado de ponto de bifurcação, os pontos críticos se juntam, ou se separam, e soluções de equilíbrio podem ser perdidadas ou podem aparecer. Pontos de bifurcação são de grande interesse em muitas aplicações porque, perto deles, a natureza das soluções da equação diferencial subjacente muda bruscamente. Por exemplo, em mecânica dos fluidos, um fluxo suave (laminar) pode se dispersar e se tornar turbulento. Ou uma coluna com carga axial pode empenar, subitamente, e exibir um grande deslocamento lateral. Ou, quando a quantidade de um dos produtos químicos em uma mistura aumenta, podem aparecer, subitamente, padrões de diversas cores em ondas espirais em um fluido originalmente quieto. Os problemas de 25 a 27 descrevem três tipos de bifurcação que podem ocorrer em equações simples da forma (i).
25. Considere a equação
(a) Encontre todos os pontos críticos da Eq. (ii). Note que não existem pontos críticos se , existe um ponto crítico se e existem dois pontos críticos, se
(b) Desenhe a reta de fase em cada caso e determine se cada ponto crítico é assintoticamente estável, semiestável ou instável.
(c) Em cada caso, desenhe diversas soluções da Eq.(ii) no plano .
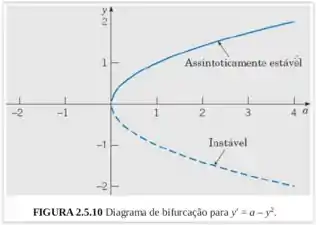
(d) Se fizermos o gráfico da localização dos pontos críticos em função de no plano , obteremos a Figura 2.5.10, chamada de diagrama de bifurcação para a Eq.(ii). A bifurcação em é chamada de bifurcação nó de sela. Esse nome é mais natural no contexto de sistemas de segunda ordem, que serão discutidos no capítulo 9.
Passo 1
Meus deus, que questão gigante. Nem quero mais faze-la, mas fazer o que...
Neste primeiro passo ficamos só com a parte que nos assustamos com o tamanho da questão, mas vamos já indicar que ela é trabalhosa, não difícil.
Passo 2
(a) Para sabermos quais são os pontos de equilíbrio de uma função, basta tomarmos quando sua derivada é nula, neste casa
Ou seja
Assim temos que, para , temos e . Para , temos . E para , não temos raízes reais, e como estamos trabalhando no conjunto dos reais, dizemos que não a pontos de há pontos de equilíbrio para essa condição.
Passo 3
(b)
Para determinar a estabilidade dos pontos, devemos calcular a derivada segunda e analisar como cada ponto se comporta em seu contorno.
Tome que
Assim temos que
Para , temos que a derivada segunda é sempre negativa e torno deste ponto definindo assim um ponto instável. Para a nossa derivada segunda é sempre positiva em torno do ponto definindo um ponto estável. E para temos que o ponto é dito semi estável, visto que a derivada segunda também é nula.
Passo 4
(c) O item solitita que extrapolamos o desenho feito no item (b) para mais algumas solução. Como isso já está bem definido no item (b), fica pra você desenhar no caderno, se achar que é necessário hahaha.
Passo 5
(d) Se tomarmos nossa função
Temos que ela é uma parábola para a direita no plano , assim como sugere o enunciado e a Figura 2.5.10. Não temos muito que resolver neste item, a não ser observar nossa função e perceber o que foi apresentado.
Resposta
Ei, a resposta está no passo a passo :)