Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.9 - Ex. 32
32 (a)Esboce o gráfico de começando pelo gráfico de e usando as transformações da Seção 1.3.
Use o gráfico da parte para esboçar o gráfico
(c)Use a definição de derivada para encontrar Quais os domínios de e ?
Use um recurso gráfico para fazer o gráfico e compare com o esboço de
Passo 1
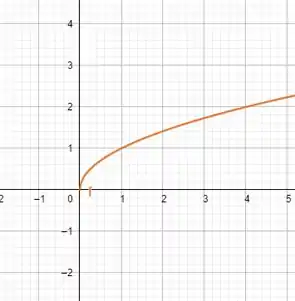
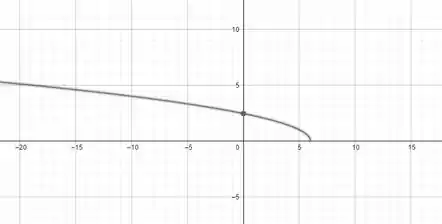
Para a questão de letra (a), vamos começar fazendo o gráfico de :
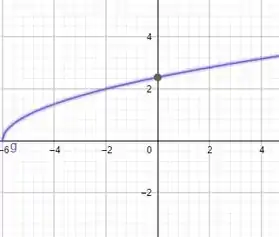
Agora tornaremos em e o gráfico fica deslocado 6 unidades para a esquerda, dessa forma:
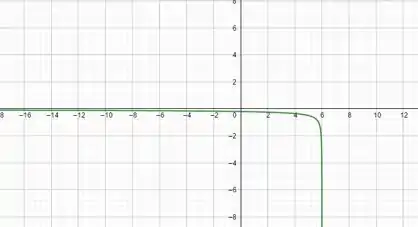
Para finalizar essa parte, vamos fazer com que se torne , quando isso acontece o gráfico fica refletido em relação a , dessa forma:
Passo 2
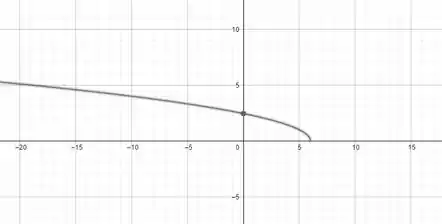
Desenharei o gráfico com algumas tangentes, para enxergarmos melhor como fica o gráfico de .
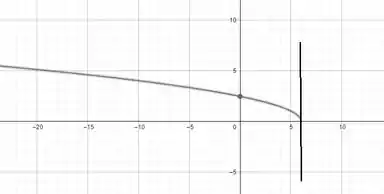
Tangente Vertical, não existe nesse ponto de abscissa
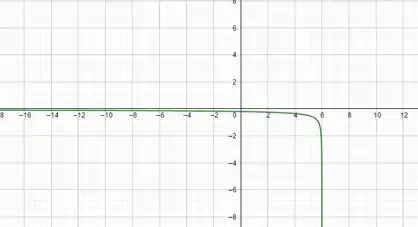
As tangentes são negativas para qualquer ponto e é também decrescente.
Gráfico de conforme as informações anteriores.
Inicialmente, vamos determinar o domínio da função . Você lembra que todo valor dentro da raiz quadrada tem de ser maior ou igual a zero? Se não lembrar, anota isso em algum lugar e vamos em frente!
Então teremos que:
Multiplicando por e numa inequação quando fazemos isso, mudamos a orientação do sinal , que vira .
Esse é o domínio de :
Passo 3
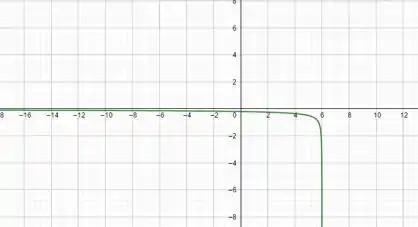
Agora, vou deixar esse passo para fazermos a derivada e o gráfico da derivada.
Anotarei aqui as expressões na equação acima:
Substituindo tudo na integral acima, temos:
Multiplicaremos no numerador e no denominador por
Fazendo essa operação de baixo agora!
(
Cortando o do numerador com o do denominador, temos:
O domínio dessa função é parecido com o domínio da função sem ser derivada, a única diferença é que agora o não vai poder ser igual a , pois se ele fosse teríamos no denominador.
Então,
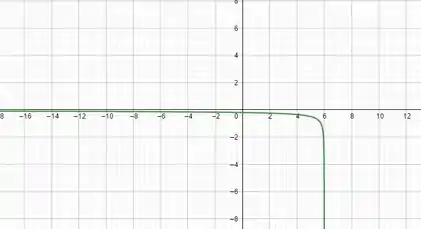
Resposta
(a)
(c)
(d)
