Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.2 - Ex. 4

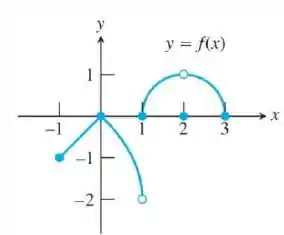
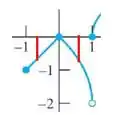
Quais das afirmações a seguir com relação à função representada graficamente aqui são verdadeiras? E quais são falsas?

não existe

não existe

existe em todo em

existe em todo em

Passo 1

Questão envolvendo limite num ponto e gráfico só tem uma coisa a se fazer: olhar o gráfico da função um pouco a esquerda (vamos chamar isso de ) e um pouco a direita (vamos chamar isso de ) de .

Se os gráficos coincidirem, ótimo o limite existe e vale o valor do gráfico naquele ponto! Se não coincidir o limite não vai existir!

Essa questão envolve 2 pontos () e depois dois intervalos: e . Então vamos calcular esses limites separadamente e depois analisamos as afirmações que ele deu!

Passo 2

Como o limite é pedido no ponto , vamos olhar o gráfico nesse ponto:

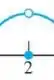
Olhando pela esquerda, vemos que a função se aproxima de 1, ou seja:

Olhando pela direita, vemos que a função se aproxima de 1, ou seja:

Como os limites deram iguais, temos que:

OBS: Só olhamos os valores da função ao redor do ponto e não exatamente o valor da função no ponto, ok?! Mesmo , ao redor do ponto a função está indo para que é o valor do limite.

Passo 3

b) Como o limite é pedido no ponto , vamos olhar o gráfico nesse ponto:

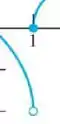
Olhando pela esquerda, vemos que a função se aproxima de -2, ou seja:

Olhando pela direita, vemos que a função se aproxima de 0, ou seja:

Tá vendo como deu diferente? Então o limite não existe!

Passo 4

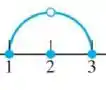
Vamos olhar agora para o intervalo como um todo. Desenhei ele aqui embaixo para ficar mais fácil:

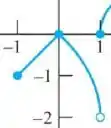
Para todos os pontos nesse intervalo, a função se aproxima sempre dos mesmos valores tanto pela esquerda quanto pela direita, então o limite existe para todos os valores! Eu fiz dois gráficos aqui embaixo: peguei um ponto qualquer entre e e depois outro ponto qualquer entre e só para você ter certeza de que o limite vai existir de fato.

Mais uma coisa interessante que podemos dizer desse caso específico é que para essa função, nesse intervalo, o limite vai sempre coincidir com o valor da função! (Nem sempre isso acontece, já vimos no passo 2 um contra-exemplo :D)

Passo 5

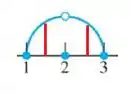
Vamos olhar agora para o intervalo como um todo. Desenhei ele aqui embaixo para ficar mais fácil:

Para todos os pontos nesse intervalo, a função se aproxima sempre dos mesmos valores tanto pela esquerda quanto pela direita, então o limite existe para todos os valores! Eu fiz dois gráficos aqui embaixo: peguei um ponto qualquer entre e 2 e depois outro ponto qualquer entre e só para você ter certeza de que o limite vai existir de fato.