Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 6.1 - Ex. 1c
Calcule.
Passo 1
Para calcular esse limite vamos usar que:
se
Temos que podemos fazer uma mudança de variável:
Assim, para :
Nesse limite temos que tende a zero para , pois quanto maior o valor de , mais próximo de zero vai está:
Vamos ver isso graficamente com a expressão com :
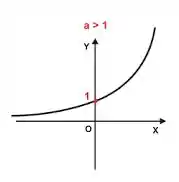
Vemos pelo gráfico que quando os valores da função tendem a zero, assim:
Resposta
Exercícios de Livros Relacionados
Cada um dos Exercícios 15-30 dá uma função f ( x ) e números L , x 0 e ϵ0 . Em cada caso, determine um intervalo aberto em torno de x 0 em que a desigualdade f x - Lϵ seja verdadeira. Dê então um valo
38- Prove as afirmações de limite nos Exercícios 37-50 lim x → 3 3 x - 7 = 2
Cada um dos Exercícios 31-36 dá uma função f ( x ) , um ponto x 0 e um número positivo ϵ . Determine L = lim x → x 0 f ( x ) . Em seguida, determine um número δ0 de modo que para todo x . 0x - x 0δ
37- Prove as afirmações de limite nos Exercícios 37-50 lim x → 4 9 - x = 5
Cada um dos Exercícios 15-30 dá uma função f ( x ) e números L , x 0 e ϵ0 . Em cada caso, determine um intervalo aberto em torno de x 0 em que a desigualdade f x - Lϵ seja verdadeira. Dê então um valo