Agora amplie a janela de visualização por . Deseja revisar sua estimativa para ?
Passo 1
Bom galera, a gente vai pegar o gráfico da nossa função naquele retângulo, e ele fica bem assim:
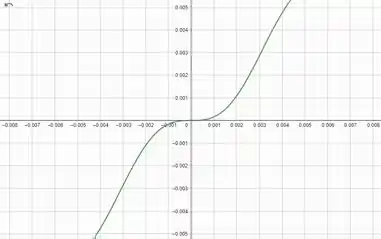
Passo 2
E se a gente notar a inclinação no ponto (a origem), no nosso gráfico, a gente vai ver que é de .
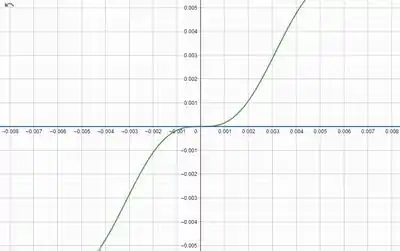
E esse coeficiente angular que é a mesma derivada é a tangente desse ângulo:
Percebeu que é diferente do resultado das letras anteriores? O que essa questão quer dizer pra gente é que encontrar a inclinação por gráfico sempre é imprecissa, mas quando maior o zoom mais precisa fica.
Mas quando a gente usa a derivada em si é como a gente estivesse no zoom máximo calculando a inclinação com a maior precissão possível. Essa imprecisão tende a .