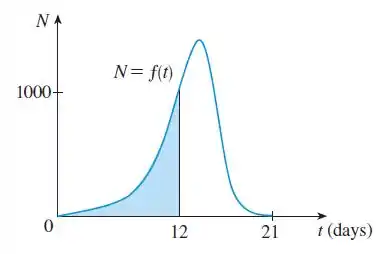
Em alguém infectado com sarampo, o nível de vírus (medidos em número de células infectadas por mL de plasma sanguíneo) atinge um pico de densidade em cerca de dias (quando uma erupção cutânea aparece) e depois diminui rapidamente como resultado de resposta imune. A área sob o gráfico de de e (como mostrado na figura) é igual ao total da quantidade de infecção necessária para desenvolver sintomas (medidas em densidade de células infectadas x tempo). A função foi modelado pela função

Use este modelo com seis subintervalos e seus pontos médios para estimar a quantidade total de infecções necessária para desenvolver sintomas de sarampo.

Vamos lá, vamos encontrar uma estimativa usando pontos médios, como vamos usar retângulos temos que , assim:

Temos que:

Aqui nós sabemos que e são os limites de integração, assim:

Vamos calcular o somatório:

Pronto, temos que o total de infecções necessária para desenvolver sintomas de sarampo é de células infectadas por mL de plasma sanguíneo.