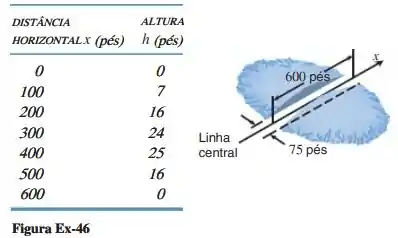
Engenheiros querem construir uma estrada reta e nivelada, com de comprimento e de largura, fazendo um corte através de um morro (veja a figura a seguir). As alturas do morro acima da linha central da estrada proposta, obtidas de vários pontos de um mapa topográfico da região, estão na tabela que segue. Para estimar o custo da construção, eles precisam conhecer o volume de terra que deve ser removido. Aproxime esse volume, arredondando ao pé cúbico mais próximo. [Sugestão: Primeiramente, estabeleça uma integral para a área da seção transversal do corte ao longo da linha central da estrada; depois, suponha que a altura do morro não varie entre a linha central e as margens da estrada.]

E aíííí, galerinha! Prontos pra mais um exercício com o Responde Aí?

Bom, para esse exercício em questão, a ideia é bem simples. Vamos resolver da maneira mais trivial: apenas calculando a integral aplicando a fórmula da regra citada.

Lembrando que a fórmula da aproximação é dada por:

Para esse caso temos os seguintes valores:

Além disso, o método da aproximação é uma representação de uma integral como mostramos a seguir:

Porém, como não é fácil para nós calcularmos o volume dessa região da estrada de forma direta, vamos dividir em duas partes como sugerido pelo enunciado: estabelecer uma integral para calcular a área da seção transversal do corte ao longo da linha central, ou seja:

Que possa ser aproximada pela regra de Simpson.

Neste caso, será a variável altura da estrada, pois a seção transversal do corte tem uma área de .

E, em seguida, supondo que a altura do morro não se altere, vamos multiplicar essa área pela largura da estrada a fim de encontrar um volume aproximado ao desejado.