Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.7 - Ex. 45
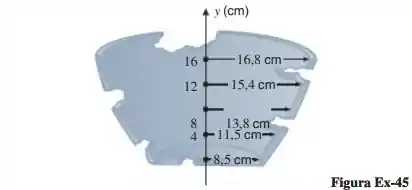
As medidas de um caco de cerâmica descoberto em uma escavação arqueológica revelam que ele veio de um pote com uma base plana e secção transversal circular (ver figura a seguir). A figura mostra medidas do raio interior do caco feitas a cada a partir da base em direção ao topo. Use esses valores para aproximar o volume interno do pote até o décimo de litro mais próximo . [Sugestão: Use (volume por secção transversal) para estabelecer uma integral apropriada para ao volume.]
Passo 1
E aíííí, galerinha! Prontos pra mais um exercício com o Responde Aí?
Bom, para esse exercício em questão, a ideia é bem simples. Vamos resolver da maneira mais trivial: apenas calculando a integral aplicando a fórmula da regra citada.
Lembrando que a fórmula da aproximação é dada por:
Para esse caso temos os seguintes valores:
Além disso, o método da aproximação é uma representação de uma integral como mostramos a seguir:
Por conta disso, vamos utilizar a integral do resultado (pode ser visto na página do livro Cálculo Vol. - Ed – ANTON) como a integral a ser aproximada pela regra de Simpson. Logo:
Onde é a área da seção transversal do sólido.
Passo 2
Como dito no enunciado, temos que a seção transversal é circular e plana. Por isso, a área dessas seções terão a fórmula de um círculo:
Isso pode ser representado pela aproximação pela regra de Simpson com a fórmula:
Passo 3
Então, a aproximação se dará por:
Portanto: