Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.3 - Ex. 27
Algumas das maiores marés no mundo acontecem na Baia de Fundy, na costa atlântica do Canada. No Hopewell Cape, a profundidade da água na maré baixa é cerca de 2,0m e na maré alta é cerca de 12,0m. O período natural de oscilação é de 12 horas e em 30 de Junho de 2009, a maior maré ocorreu às 6:45. Encontre uma função envolvendo a função cosseno que modele a profundidade da água em metros em função do tempo (em horas a partir da meia noite) naquele dia.
Passo 1
Eaeee, belezinha?? Bom... a questão quer que encontremos uma função envolvendo a função cosseno que modele a profundidade da água em metros em função do tempo (em horas a partir da meia noite).
Nesse sentido a nossa função terá uma parte constante (que é a média do nível de água) e uma parte variável dada pelo cosseno.
Como a maré faz como que o nível da água oscile com o passar do tempo, vamos escolher uma função que modele esse movimento harmônico que vai ser nesse estilo aqui:
Onde é a amplitude total da maré, ou seja, a metade da diferença entre a maior e a menor maré.
E aí?? Bora lá?? 😉
Passo 2
Vamos entender quem é quem na nossa função.
Bom pessoal, a amplitude desta função pode ser encontrada pela metade da diferença entre a maior e a menor maré. Então:
A média da amplitude (o centro) é dado por:
Foi dito no enunciado que o período é de , assim teremos .
A maior maré ocorreu as , ou seja .
Como o enunciado pede para que a nossa função seja uma função do tipo , vamos escolher esse ponto de máxima maré para ser nosso , e não precisarmos de defasagens.
Perfeito.
Passo 3
Lembrando que a forma da equação é dada por:
Podemos então substituir os valores que acabamos de encontrar diretamente na função, e teremos:
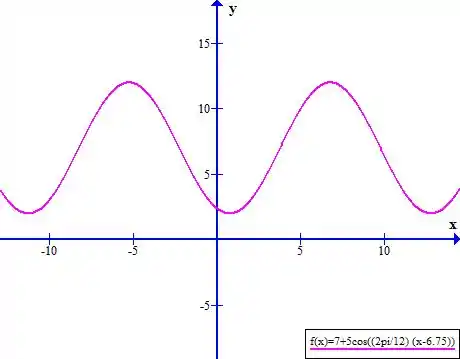
Graficamente, a nossa função é dada da seguinte forma:
