Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.1 - Ex. 11
Alguns sistemas de computação algébrica têm comandos que traçam retângulos aproximantes e calculam as somas de suas áreas, pelo menos se for uma extremidade esquerda ou direita. (Por exemplo, no Maple use leftbox, rightbox, leftsum e rightsum.)
(a) Se , encontre as somas esquerda e direita para e .
(b) Ilustre fazendo o gráfico dos retângulos da parte (a).
(c) Mostre que a área exata sob está entre e .
Passo 1
Fala aí, galerinha! 😉
Bom, essa questão fala para gente que alguns sistemas de computação algébrica têm comandos que traçam retângulos aproximantes e calculam as somas de suas áreas, pelo menos se por uma extremidade esquerda ou direita.
Por exemplo, no Maple use leftbox, rightbox, leftsum e rightsum.)
Teremos que responder a alguns itens usando esses sistemas. Sendo eles:
No item (a), temos que
Se , encontre as somas esquerda e direita para e .
No item (b), precisaremos ilustrar fazendo o gráfico dos retângulos da parte (a).
E no item (c), vamos mostrar que a área exata sob está entre e .
Passo 2
No Maple, nós temos que executar um número de passos antes de conseguir uma resposta numérica. Depois de carregar o pacote de estudante com nós usamos o comando
o que nos dá a expressão em notação de soma.
Para termos a aproximação da soma, nós usamos
Matemática não tem um comando especial para essas somas, então nós devemos digitá-las manualmente. Por exemplo:
A primeira soma esquerda é dada por
e nós usamos o comando no que se resulta para termos uma aproximação numérica.
Na Derivada, nós usamos o comando
para ter as somas esquerdas, mas devemos decidir as somas direitas por nós mesmos.
Veja só! 😉
Passo 3
Item a).
Com , as somas esquerdas estão sob a forma:
Então, especificamente,
As somas direitas estão sob a forma:
Então, especificamente:
Tranquilo até aqui? 😁
Passo 4
Item b). Pontos extremos esquerdos:
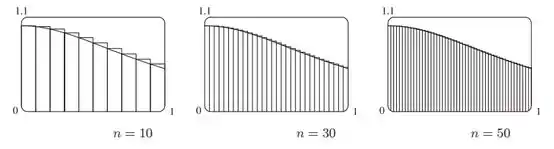
Pontos extremos direitos:
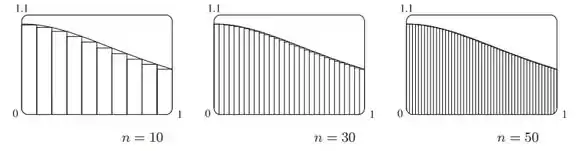
Passo 5
Item c).
Nós sabemos que desde que
é uma função decrescente em , todas as somas esquerdas são maiores do que a área real, e todas as somas direitas são menores.
Desde que a soma esquerda com
está entre
e a soma direita, também com
está entre
nós concluímos que
logo, a área exata está entre
E aí! entendeu tudo? Responde Aí! 😇
Resposta
a)
b)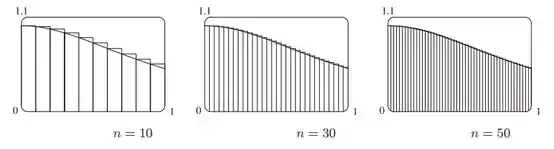 
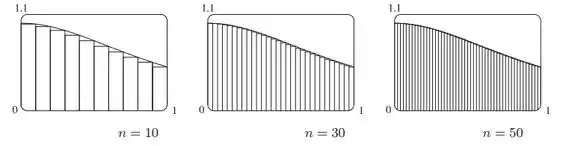
c) entre e .