Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.7 - Ex. 27
A tabela da a população mundial no século XX
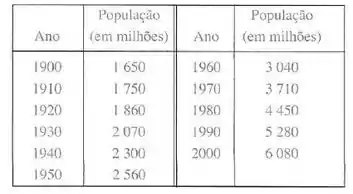
- Estime a taxa de crescimento populacional em 1920 e em 1980 fazendo a média das inclinações de duas retas secantes.
- Use uma calculadora gráfica ou um computador para achar uma função cúbica (um polinômio de terceiro grau) que modele os dados (veja a seção 1.2).
- Utilize o modelo da parte (b) para achar um modelo para a taxa de crescimento populacional no século XX
- Use a parte (c) para estimar as taxas de crescimento em 1920 e em 1980. Compare com sua estimativa da parte (a).
- Estime a taxa de crescimento em 1985.
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada uma tabela que nos dá a população mundial em função do ano
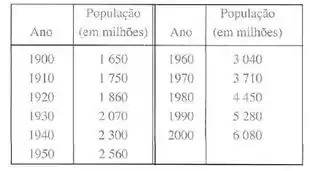
A partir dessa tabela, nosso objetivo é estimar a taxa de crescimento em e em pelas médias das inclinações das duas retas secantes. A partir de uma calculadora gráfica obter a função cúbica da função e a partir dessa função, determinar a função taxa de crescimento e refazer os cálculos do item a) e estimar a taxa de crescimento em .
Parece complicado?
Para resolver esse problema vamos, primeiramente, calcular as medias das das inclinações em volta do ano que estamos calculando pela equação
Pra isso calculamos a variação posterior e entreior ao ano e depois calculamos as médias dos resultados.
Depois vamos utilizar uma calculadors gráfica para obter a função de terceiro grau que melhor descreve a função da tabela e a partir dessa função, calculamos sua derivada para obter a função taxa de crescimento e por ultimo substituímos os anos na variavel dessa função.
Veja só!
Passo 2
Para estimar nesses dois anos, calcularemos dois consecutivos e tiraremos a média deles, para isso sabemos que
Entre 1920 e 1930, temos
Entre 1920 e 1910, temos
Tirando a média, ficamos com
Entre 1980 e 1990, temos
Entre 1980 e 1970, temos
Tirando a média, ficamos com
Tranquilo até aqui?
Passo 3
Utilizando uma calculadora gráfica, de acordo com a seção 1.2, podemos calcular os coeficientes do polinômio do 3º grau que se ajusta aos dados, temos que
Daí, calculando pela calculadora, ficamos com
Ou seja
Show?
Passo 4
Se derivamos teremos o modelo para a taxa de crescimento
Pela regra da potencia, ficamos com
Onde
Bacana, não é?
Passo 5
Para estimarmos as taxas em 1920 e em 1980, basta substituirmos por estes valores na expressão de
Para 1920
Anteriormente encontramos e estes dois valores são bem próximos.
Para 1980
Anteriormente encontramos estes dois valores são bem próximos.
Estamos quase no fim!
Passo 6
Podemos calcular a taxa de crescimento nesse ano usando . Daí, temos que
É isso! O que achou? Responde Aí!
Resposta
a) ,
b)
c)
d) ,
e)