Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 14.4 - Ex. 22

A altura h de ondas em mar aberto depende da velocidade do vento v e do tempo t durante o qual o vento se manteve naquela intensidade. Os valores da função h = f   ( v , t ) são apresentados na seguinte tabela.

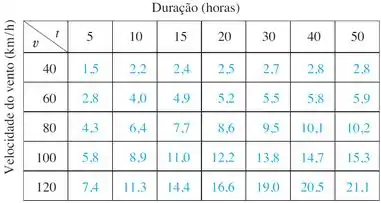
Use a tabela para determinar uma aproximação linear da função altura da onda quando v está próximo de 80   k m / h e t está próximo de 20 horas. Em seguida, estime a altura das ondas quando está ventando por 24 horas a 84   k m / h .

Passo 1

Show de bola, galera! Nessa questão nós temos uma tabela de valores que fornecem a altura h de ondas em mar aberto em função da velocidade do vento ( v ) e do tempo ( t ) em que o vento se manteve nessa velocidade.

Com isso, a questão quer que a gente determine uma aproximação linear da função altura ( h ) no ponto 80,20   para depois estimar a altura das ondas quando está ventando por 24 horas a 84   k m / h .

Muita informação, né? Então vamos com calma...

Primeiro nós precisamos obter a aproximação linear da função altura, que chamaremos de L ( v , t ) . Como nós obtemos essa função em um ponto a , b ?

Como estamos procurando uma aproximação para uma função de 2 variáveis no ponto ( a , b ) , essa aproximação será dada por:

L v , t = f a , b + f v a , b v - a + f t a , b t - b

Uma vez obtida essa aproximação no ponto a , b = 80,20 , vamos pegar o ponto 84,24   e substituir nela.

Passo 2

Aqui nós vemos que serão necessárias as derivadas da função h = f ( v , t ) para obter L v , t .

Essas derivadas parciais nós vamos obter utilizando a noção de derivada por limites.

Lembre-se: se queremos obter f v = ∂ f / ∂ v , temos que manter a variável t fixa e fazer pequenas variações em torno de v , ou seja,

f v = lim Δ v → 0 ⁡ f v + Δ v ,   t - f v , t Δ v

Da mesma forma, para calcular f t = ∂ f / ∂ t , temos que manter a variável v fixa e fazer pequenas variações em torno de t , isto é,

f t = lim Δ t → 0 ⁡ f v ,   t + Δ t - f v , t Δ t

Lembrou? Beleza.

Passo 3

Agora vamos relembrar o procedimento que a gente pode utilizar para calcular uma aproximação para derivada quando temos diversos valores de função apresentados igual aos que estão na tabela do enunciado.

Pelo que discutimos no passo 2, temos que focar no ponto (80,20) e fazer as menores variações em torno dele.

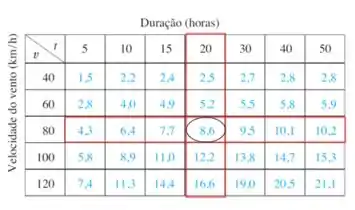
Na tabela acima,está destacado o valor de h = f ( 80,20 ) .

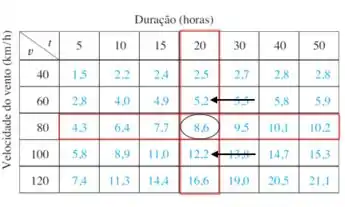
Para começar calculando f v 80,20 , vamos então manter t = 20 h fixo e fazer variações em v .   A menor variação possível em v vai nos levar aos pontos ( 60,20 ) e ( 100,20 ) , cujos valores de h estão indicados na imagem abaixo:

Temos dois valores próximos para fazer a estimativa da derivada, então vamos usar cada um deles e depois fazer a média dessas estimativas, ok?

f v , 1 80,20  estimativa 1 para  f v 80,20

f v , 2 80,20  estimativa 2 para  f v 80,20

A partir disso,

f v 80,20 ≅ f v , 1 80,20 + f v , 2 80,20 2

Vamos seguir o mesmo raciocínio para calcular f t ( 80,20 ) . Os valores que usaremos estão indicados na imagem abaixo:

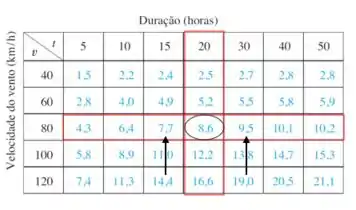
Vamos fazer o seguinte:

f t , 1 80,20  estimativa 1 para  f t 80,20

f t , 2 80,20  estimativa 2 para  f t 80,20

f t 80,20 ≅ f t , 1 80,20 + f t , 2 80,20 2

Agora vamos às contas...

Passo 4

Primeiro vamos fazer para f v 80,20   usando os valores da tabela:

f v , 1 80,20 = f 100,20 ⏞ 12,2 - f 80,20 ⏞ 8,6 20 = 0,18

f v , 2 80,20 = f 60,20 ⏞ 5,2 - f 80,20 ⏞ 8,6 - 20 = 0,17

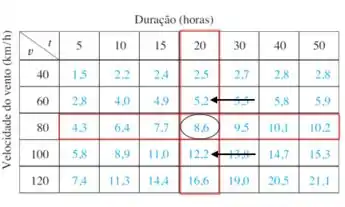
Fazendo a média entre os dois resultados, temos

f v 80,20 ≅ f v , 1 80,20 + f v , 2 80,20 2

f v 80,20 ≅ 0,18 + 0,17 2 = 0,175

Passo 5

Agora usamos a tabela abaixo para estimar f t 80,20 :

f t , 1 80,20 = f 80,30 ⏞ 9,5 - f 80,20 ⏞ 8,6 10 = 0,09

f t , 2 80,20 = f 80,15 ⏞ 7,7 - f 80,20 ⏞ 8,6 - 5 = 0,18

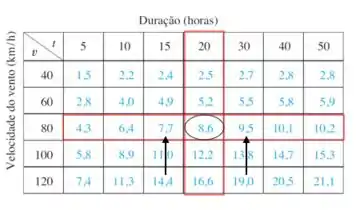
Assiiimm....

f t 80,20 ≅ f t , 1 80,20 + f t , 2 80,20 2

f t 80,20 ≅ 0,09 + 0,18 2 = 0,135

Passo 6

Finalmente, vamos escrever a expressão da aproximação linear da função no ponto 80,20 :

f x , y ≈ f 80,20 + f x 80,20 x - 80 + f y 80,20 y - 20

f x , y ≈ 8,6 + 0,175 x - 80 + 0,135 y - 20

Para a aproximação que queremos no enunciado:

f 84,24 ≈ 8,6 + 0,175 84 - 80 + 0,135 24 - 20 = 9,84

Resposta

f x , y ≈ 8,6 + 0,175 x - 80 + 0,135 y - 20

f 84,24 ≈ 9,84

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre as linearizações L(x, y, z) das funções nos Exercícios 39-44 nos pontos determinados. f x , y , z = e x + c o s c o s( y + z ) a ) ( 0,0 , 0 ) b )0 , π 2 , 0 c ) 0 , π 4 , π 4
Nos Exercícios 33-38, encontre a linearização L(x, y) da função ƒ(x, y) em P0. Em seguida, encontre um limitante superior para a magnitude |E| do erro na aproximação ƒ(x, y) ≈ L(x, y) sobre o retângul
Nos Exercícios 25-30, encontre a linearização L(x, y) da função em cada ponto. f x , y = x 3 y 4e m a ( 1 , 1 ) b ( 0 , 0 )
Nos Exercícios 33-38, encontre a linearização L(x, y) da função ƒ(x, y) em P0. Em seguida, encontre um limitante superior para a magnitude |E| do erro na aproximação ƒ(x, y) ≈ L(x, y) sobre o retângul
Nos Exercícios 45-48, encontre a linearização L(x, y, z) da função ƒ(x, y, z) em P0. Em seguida, encontre um limitante superior para a magnitude do erro E na aproximação ƒ(x, y, z) ≈ L(x, y, z) sobre