Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.6 - Ex. 53
Um aluno quer encontrar a área delimitada pelos gráficos de .
a) Mostre que a área exata é .
b) O aluno usa uma calculadora para aproximar o resultado da parte a) até a segunda casa decimal e obtém a resposta incorreta de . Qual foi o erro dele? Encontre a aproximação correta.
Passo 1
a) Então galera, antes de escrevermos uma integral para resolver nosso problema, primeiro seria interessante esboçar o gráfico da região em questão para podermos visualizar com mais facilidade a área que estamos trabalhando. Nossa função é:
E o intervalo é: . Sendo assim, teremos:
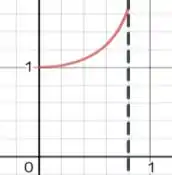
Então a área que queremos descobrir é essa abaixo da curva vermelha, no qual é limitada pelo intervalo dado e . Show!
Passo 2
Escrevendo nossa integral:
Mas como resolvemos essa integral, galera? O resultado dessa integral é tabelado, então não precisamos nos preocupar, ok? A resposta é essa aqui:
Aplicando o Teorema Fundamental do Cálculo (Parte 1), teremos:
Logo:
E essa é nossa área, assim como o enunciado indica!
Passo 3
b) Então galera, se utilizarmos uma calculadora para calcular encontraremos, de fato, (aproximando para duas casas decimais). No entanto, esse é o valor da área em graus! Onde já se viu uma área medida em graus, galera? A resposta certa seria em radianos que, convertendo, seria:
E essa é a aproximação correta! 😉
Resposta
a)
b) Aproximação correta: .