Analisar graficamente a existência de assíntotas para as seguintes funções:
Passo 1
O gráfico dessa questão fica com essa cara aqui:
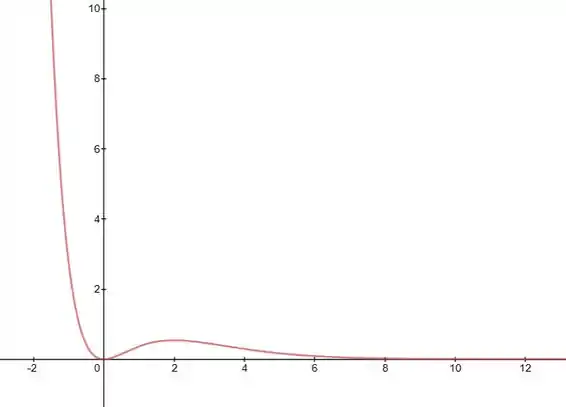
Passo 2
Analisando o gráfico, já vemos que é uma assíntota horizontal. Agora resta saber se aquela parte do gráfico que tá subindo é uma assíntota vertical. Pra isso, pensa em qual valor negativo tem que botar na função pra ela devolver um valor infinito:
Isso aconteceria no ponto em que o denominador tender a , mas isso só é atingido para tendendo a menos infinito! Por isso, essa não é uma assíntota, e ficamos só com a horizontal.
Resposta
é uma assíntota horizontal.