Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.1 - Ex. 35
Analise as funções trigonométricas nos intervalos especificados indicando onde é crescente, decrescente, côncava para cima, côncava para baixo, e as coordenadas de todos os pontos de inflexão. Verifique se seus resultados estão em conformidade com o gráfico de gerado por algum recurso computacional.
35.
Passo 1
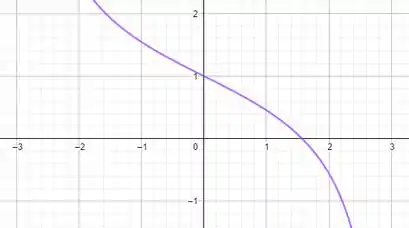
Peguemos o gráfico da função, dentro do intervalo pedido, pra já termos uma melhor ideia dos nossos resultados:
Passo 2
Pelo gráfico já podemos afirmar que é sempre decrescente, pois os valores de sempre crescem da esquerda pra direita. O intervalo então será:
Passo 3
No intervalo observado, não é crescente em nenhuma parte. Logo, não há intervalo!
Passo 4
Pra verificar os intervalos de concavidade voltada pra cima e pra baixo, precisamos dos pontos de inflexão, que se determinam quando igualamos a derivada segunda da função a zero.
Temos:
Igualando a zero, vamos ter:
Temos duas possibilidades:
ou
Resolvendo elas, respectivamente:
Tirando a raiz:
Da trigonometria, não existem quaisquer ângulos cuja secante valha 0. Assim, nos resta a segunda opção de resposta:
Pra que a tangente de um ângulo valha zero, esse ângulo precisa ser zero. Assim:
Passo 5
Logo, em temos o nosso ponto de inflexão.
Assim, os intervalos de concavidade voltada pra cima e pra baixo são:
Pra cima:
Pra baixo:
Resposta
Ei, a resposta está no passo a passo :)