Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.1 - Ex. 37
Analise as funções trigonométricas nos intervalos especificados indicando onde é crescente, decrescente, côncava para cima, côncava para baixo, e as coordenadas de todos os pontos de inflexão. Verifique se seus resultados estão em conformidade com o gráfico de gerado por algum recurso computacional.
37.
Passo 1
Peguemos o gráfico da função, dentro do intervalo pedido, pra já termos uma melhor ideia dos nossos resultados:
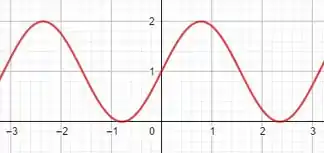
Passo 2
vai ser crescente entre os pontos de mínimo e os pontos de máximo, nesta ordem, necessariamente. Pra determiná-los, precisamos derivar a função e igualar a derivada a zero.
Temos:
Igualando a zero, vamos ter:
Do ciclo trigonométrico, sabemos que os ângulos que atendem essa relação são o de e todos os arcos que distem desse ângulo.
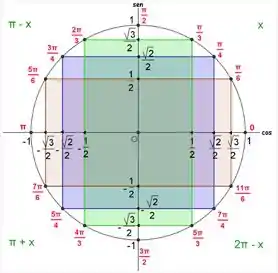
Como estamos considerando o intervalo , a partir de , os ângulos que atendem a essa relação serão:
, , e
Passo 3
Assim, obserando o gráfico, temos os intervalos em que a função cresce e decresce:
Crescente:
Decrescente:
Passo 4
Pra verificar os intervalos de concavidade voltada pra cima e pra baixo, precisamos dos pontos de inflexão, que se determinam quando igualamos a derivada segunda da função a zero.
Temos:
Igualando a zero, vamos ter:
Temos duas possibilidades:
ou
Resolvendo elas, considerando o intervalo trabalhado, temos respectivamente:
, e
, e
Assim, considerando os pontos e observano atentamente ao gráfico, os intervalos de concavidades serão:
Pra baixo:
Pra cima:
Resposta
Ei, a resposta está no passo a passo :)