Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.3 - Ex. 62

(a) Use um gráfico de f para fornecer uma estimativa aproximada dos intervalos de concavidade e as coordenadas dos pontos de inflexão.

(b) Use um gráfico de f ' ' x para obter melhores estimativas.

f x = x - 1 2 x + 1 3

Passo 1

E aí! como vai?

Nesse problema foi dada a função:

f x = x - 1 2 x + 1 3

E nosso objetivo é plotar o gráfico de f usando uma ferramenta gráfica, estimar os intervalos de concavidade e os pontos de inflexão. Depois calculamos a segunda derivada de f e confirmamos as estimativas.

Parece complicado?

Para calcular as concavidades de uma função, temos que obter a sua derivada de segunda ordem e e determinar quando f ' ' > 0 e f ' ' < 0 .

Quando f ' ' > 0 a concavidade do gráfico da função é voltada para cima e quando f ' ' < 0 a concavidade do gráfico da função é voltada para baixo...

Já os pontos de inflexão são obtidos quando f ' ' = 0 , que é quando a função muda de concavidade.

Dito isso... bora começar!

Passo 2

Bom galera, a nossa função é:

f x = x - 1 2 x + 1 3

Então vamos dar uma olhadinha no gráfico da função agora usando uma ferramenta gráfica:

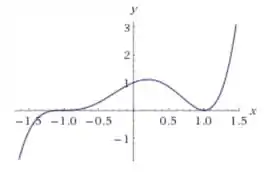
Beleza, observando o gráfico a gente consegue encontrar:

Convavidade para cima: - 1 : - 0.3 ,   0.7 : ∞

Que é o intervalo que a função vai ficar inclinando pra cima.

Convavidade para baixo: - ∞ : - 1 ,   - 0.3 : 0.7

Quando a função vai ficar inclinando pra baixo.

Pontos de inflexão: - 1 , - 0.3 , 0.7

Que são os pontos que a concavidade vai mudar.

Tranquilo até aqui?

Passo 3

Show de bola, agora vamos derivar a função duas vezes usando a regra geral e a regra da multiplicação:

f x = x - 1 2 x + 1 3

Antes disso vamos desenvolver essas potências :

f x = x 2 - 2 x + 1 x 3 + 3 x 2 + 3 x + 1

Agora sim... aplicando a regra do produto, temos:

f ' x = d x 2 - 2 x + 1 d x · x 3 + 3 x 2 + 3 x + 1 + x 2 - 2 x + 1 · d x 3 + 3 x 2 + 3 x + 1 d x

f ' x = 2 x - 2 · x 3 + 3 x 2 + 3 x + 1 + x 2 - 2 x + 1 · 3 x 2 + 6 x + 3

f ' x = 5 x 4 + 4 x 3 - 6 x 2 - 4 x + 1

E derivando novamente, usando a regra da potência:

f ' ' x = 20 x 3 + 12 x 2 - 12 x - 4

Maravilha!

Passo 4

Agora, a gente olha no gráfico da segunda derivada pra encontrar quando:

f ' ' x = 0

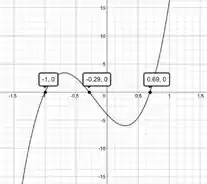
Ou seja, os pontos de inflexão são: - 1 , - 0.29 , 0.69

E com isso temos os pontos mais exatos das concavidades que são:

Convavidade para cima quando o gráfico de f ' ' é positivo: - 1 : - 0.29 ,   0.69 : ∞

Convavidade para baixo quando o gráfico de f ' ' é negativo: - ∞ : - 1 ,   - 0.29 : 0.69

É isso! entendeu tudo? Responde Aí!

Resposta

(a)

Convavidade para cima: - 1 : - 0.3 ,   0.7 : ∞

Convavidade para baixo: - ∞ : - 1 ,   - 0.3 : 0.7

Pontos de inflexão: - 1 , - 0.3 , 0.7

(b)

Convavidade para cima: - 1 : - 0.29 ,   0.69 : ∞

Convavidade para baixo: - ∞ : - 1 ,   - 0.29 : 0.69

Pontos de inflexão: - 1 , - 0.29 , 0.69

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

g) y =(x)/(1 + x^2)
f) g(x) = (x^2)/(x^2 - 2)
n) f(x) = x e^((1)/(x))
o) f (x) = x ln x
j) x^4 - 2 x^3 + 2 x