Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.3 - Ex. 25

Esboce o gráfico de uma função que satisfaça todas as condições dadas.

  1. f ' x > 0 e f ' ' x < 0 para qualquer valor de x .
  2. f ' x < 0 e f ' ' x > 0 para qualquer valor de x .

Passo 1

Oiee vamo lé

Vamos esboçar dois gráficos de funções que satisfaçam as seguintes condições:

  1. f ' x > 0 e f ' ' x < 0 para qualquer valor de x .

    2. Para esta condição, a função f ( x ) deve ser crescente e côncava para baixo em todo o seu domínio.

    Um exemplo de tal função é a função logarítmica negativa: f x = - ln ⁡ ( x )

    Derivadas:

    f ' x = - 1 x

    f ' ' x = 1 x 2

    Para x > 0 :

    - f ' x > 0     porque - 1 / x é positivo para x > 0 .

    - f ' ' x < 0 porque 1 / x 2 é sempre positivo e o sinal negativo indica concavidade para baixo.

    Passo 2

    Para esta condição, a função f ( x ) deve ser decrescente e côncava para cima em todo o seu domínio. Um exemplo de tal função é a função logarítmica negativa espelhada: f ( x ) = - e - x   .

  2. f ' x < 0 e f ' ' x > 0 para qualquer valor de x .

Derivadas:

f ' ( x )   =   e - x

f ' ' ( x )   =   - e - x

Para x ∈ R

- f ' x < 0 porque e - x   sempre positivo e o sinal negativo indica uma função decrescente.

- f ' ' x > 0 porque - e - x é sempre negativo e o sinal positivo indica concavidade para cima.

Passo 2

Esboço dos Gráficos

Gráfico 1:   f ' x >   0     e     f ' ' x <   0

A função     f x =   - l n x :

- Crescente em ( 0 ,   ∞   )

- Concavidade para baixo

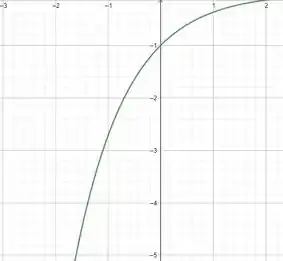
Essa função é sempre crescente e côncava para baixo.

Passo 3

Gráfico 2: f ' x < 0     e     f ' ' x > 0

A função f x = - e - x

- Decrescente em R

- Concavidade para cima

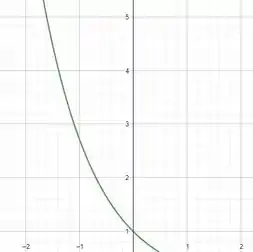
Essa função é sempre decrescente e côncava para cima.

Resposta

Vide a explicação

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre os pontos de inflexão do gráfico da função dada, se existirem. Determine onde o gráfico é côncavo para cima e onde ele é côncavo para baixo. Faça um esboço do gráfico e mostre um segmento da
Se f x = a x 3 + b x 2 , determine a e b de tal forma que o gráfico de f tenha um ponto de inflexão em ( 2 ,16 ) .
Ache o ponto (ou pontos) de inflexão do gráfico da função definida por f x = 2 - x 2 ,s ex0 x 2 + 2 ,s ex ≥ 0 e determine onde o gráfico é côncavo para cima e côncavo para baixo.
Ache o ponto (os pontos) de inflexão do gráfico da função definida por f x = x 1 5 e determine onde o gráfico é côncavo para cima e onde é côncavo para baixo.
Se f x = a x 3 + b x 2 + c x , determine a , b e c de tal forma que o gráfico de f tenha um ponto de inflexão em ( 1 ,- 1 ) e que a inclinação da tangente inflexional seja - 3 .