Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.3 - Ex. 24
Esboce o gráfico de uma função que satisfaça a todas as condições dadas
- para todo
- para todo
Passo 1
Opa! Bora pra mais uma questão?! Nessa daqui temos um desafio, precisamos desenhar dois gráficos com poucas informações. Tudo o que sabemos é:
- para todo
- para todo
Vamos relembrar o significado das derivadas! A derivada primeira, indica se a função é crescente ou decrescente. Já a derivada segunda vai nos falar se a concavidade é pra cima ou pra baixo!
Obviamente, com apenas essas informações, vamos ter soluções infinitas! Então é hora de colocar a criatividade pra jogo!
Passo 2
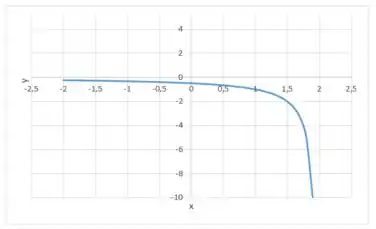
Primeiro vamos a letra (a), temos que pensar em uma função que tem para todo , ou seja, ela sempre é decrescente e sua concavidade é sempre pra baixo:
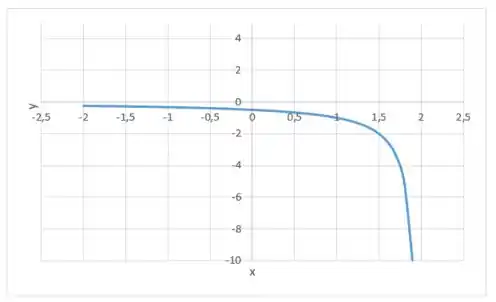
Podemos reparar que a função é decrescente e tem a concavidade pra baixo, exatamente como queríamos!
Passo 3
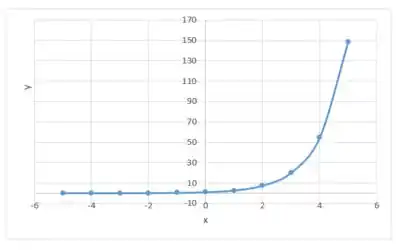
Agora vamos a uma função onde para todo . Aqui a nossa função sempre será crescente e sua concavidade sempre será pra cima!
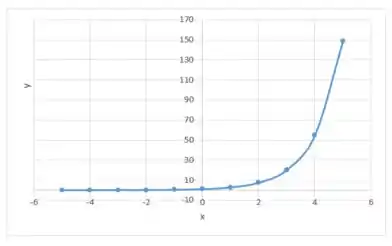
Repara que o gráfico tem exatamente o que o enunciado pediu! Mas é claro! Essa não é a única opção, existem infinitas soluções!
Resposta
