Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.3 - Ex. 66
66. No noticiário nacional da televisão, o apresentador disse, “Aqui vão boas notícias! Este ano, os resultados dos testes de desempenho diminuiram a uma taxa menor”. Interprete a afirmação do apresentador em termos de uma função e suas primeira e segunda derivadas.
Passo 1
Show de bicicletinhas galera, vamos considerar a o resultado dos testes de desempenho como uma função . E a partir daí tirar as conclusões necessárias, vem comigo!
Passo 2
Beleza, o apresentador disse que os resultados estão diminuindo a uma taxa menor, e é aí que começa a malícia, porque a palavra “taxa” se refere a variação de alguma coisa, nesse caso, a variação dos resultados. Como a gente é sagaz, essa variação é dada pela primeira derivada, logo podemos reescrever a frase como
Quer dizer que nossa primeira derivada está diminuindo. E essa é uma informação sobre a segunda derivada, já que se isso está acontecendo quer dizer que é negativa
Passo 3
Iradoso né, então quer dizer que a segunda derivada é negativa, e quando isso acontece temos uma função que é côncava para baixo, mais ou menos assim
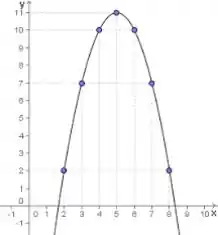
Ou seja, se pegarmos ponto a ponto seguindo a reta real , as primeiras derivadas estrão diminuindo sucessivamente.E agora o outro detalhe é se a primeira derivada é negativa ou não. E com toda malandragem do mundo, podemos observar que a frase diz que “Aqui vai boas notícias”, e para ser uma boa notícia, o desempenho teria que estar melhorando, fazendo com que, por mais que a taxa esteja diminuindo em seu valor, ela ainda seja positiva. Se a taxa é positiva, quer dizer que a primeira derivada é positiva, e portanto
