Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.Revisão - Ex. 1
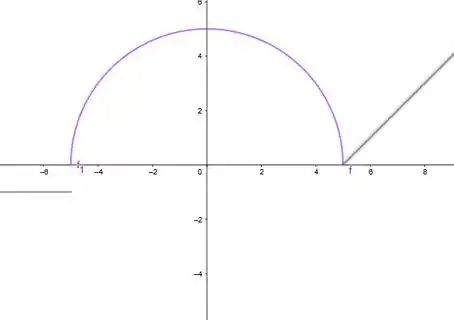
- Esboce o gráfico da função:
Passo 1
Belezoca meus amores, a função que enunciado deu pra gente é essa aqui:
Queremos traçar o gráfico dela, como ela está definida por parte, vamos analisar cada uma delas separa damente, de acordo com o dominio.
Passo 2
Saca só, na primeira parte ele diz que se , ou seja, para qualquer , e como essa função é um constante, o desenho dela vai ser mais ou menos esse aqui:
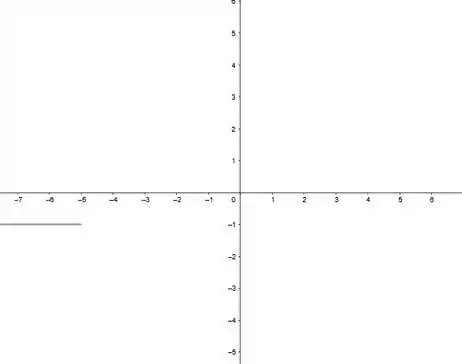
Passo 3
Agora para a segunda parte, temos que , se . Reorganizando os termos, temos:
Logo, essa equação se trata de um circunferência, de raio 5, só que só a parte de cima dela, desse jeito:
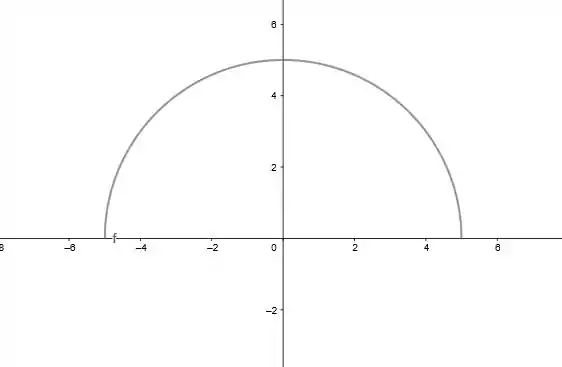
Passo 4
E por fim, para , se , temos o gráfico de uma reta, com dominio de para qualquer maior 5, desse jeitinho ó:
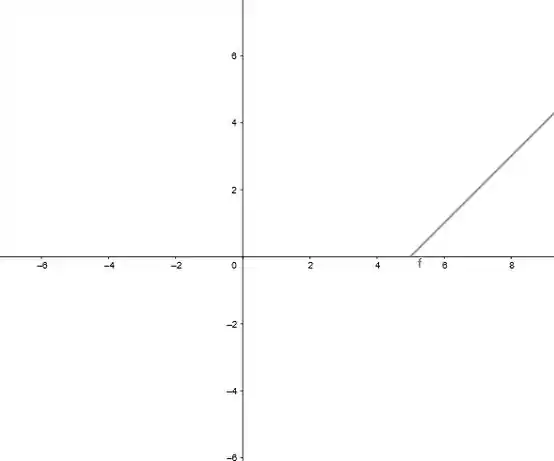
Juntando todos os gráficos que encontramos vamos obter o gráfico de , ele fica desse jeitinho ó:
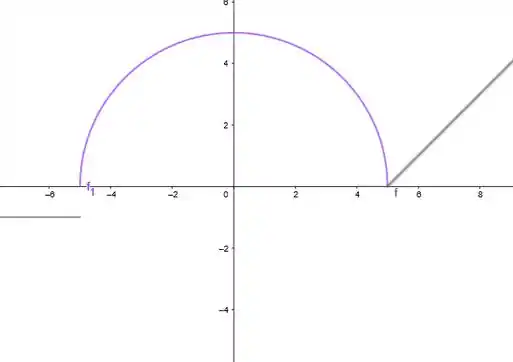
E esse é o desenho da nossa função.
Resposta
