Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.Revisão - Ex. 11
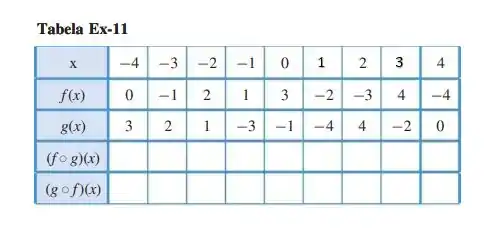
11. Complete a tabela a seguir.
Passo 1
Belezinha galera, dada a tabela:
Queremos preencher ela com os valores corretos, pra isso podemos usar os conceitos de função composta, por exemplo para a primeira linha temos:
Podemos reescrever como:
Então para , temos , e olhando na tabela vemos que , logo:
E verificando na tabela novamente vemos que , portanto:
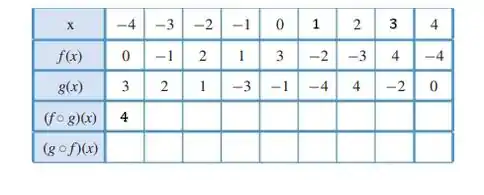
Agora fazendo isso para toda linha de , vamos ter que:
Passo 2
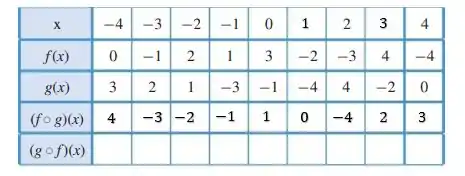
Agora para segunda linha, temos algo bem parecido, saca só, temos , e podemos reescrever como:
Para , temos que , logo:
E de acordo com a tabela, , logo:
E fazendo isso para o restante da linha, vamos obter:
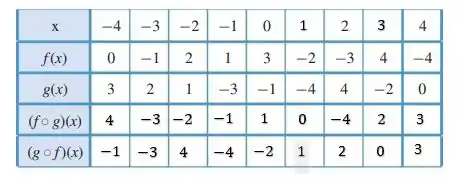
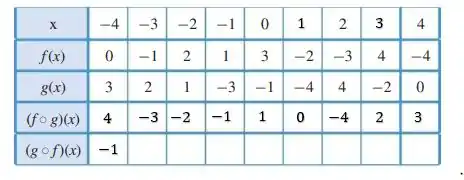
Resposta
Exercícios de Livros Relacionados
Expresse f como uma composição de duas funções; isto é, encontre g e h tais que f = g ∘ h. [Nota: Cada exercício tem mais de uma solução.](a) f x = 3 sen x 2 (b) f x = 3 sen 2 x + 4 s e n ( x )
Expresse f como uma composição de duas funções; isto é, encontre g e h tais que f = g ∘ h. [Nota: Cada exercício tem mais de uma solução.](a) f x = 1 + sen x 2 3 (b) f x = 1 - x 3
Expresse f como uma composição de duas funções; isto é, encontre g e h tais que f = g ∘ h. [Nota: Cada exercício tem mais de uma solução.](a) f x = 1 1 - x 2 (b) f x = 5 + 2 x
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.O domínio de f + g é a interseção dos domínios de f e de g.
Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.O domínio de f ∘ g consiste em todos os valores de x no domínio de g nos quais g x ≠ 0 .