Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.Revisão - Ex. 41

41. Considere f x = x 2 tan ⁡ x + ln ⁡ x ,   c o m   0 < x < π / 2 .

  1. Explique por que f é injetora.
  2. Use um recurso gráfico para exibir o gráfico de f . Depois exiba os gráficos de f e de f - 1 juntos na mesma janela. Quais são as assíntotas de cada gráfico?

Passo 1

Show de boletas, a definição de uma função injetora diz que f ( x ) é injetora se, e somente se, f c = f ( u ) implicar que c = u , ou seja, só pode haver uma solução possível para cada valor da imagem. E dado o intervalo 0 < x < π / 2 , qualquer valor distinto que pegarmos e aplicarmos na função f x = x 2 tan ⁡ x + ln ⁡ x , nos retornará outro valor distinto. Portanto f x = x 2 tan ⁡ x + ln ⁡ x é injetora.

Passo 2

E o gráfico de f x = x 2 tan ⁡ x + ln ⁡ x é:

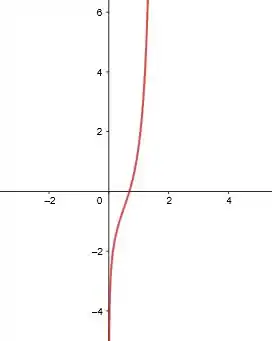
Resposta

  1. Demonstração.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o valor exato da expressão sem usar uma calculadora.
Reescreva a expressão como um único logaritmo.
Reescreva a expressão como um único logaritmo.
Faça o gráfico das funções na mesma tela de um recurso gráfico computacional. [Use a fórmula de mudança de base quando necessário.]
Use as propriedades de logaritmos do Teorema 0.5.2 para reescrever a expressão em termos de r , s e t , sendo r = ln ⁡ a , s = ln ⁡ b e t = ln ⁡ c .