Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.3 - Ex. 64

64. Aproximação É muito útil saber que, quando é medido em radianos, para valores de numericamente pequenos. Na Seção 3.11, veremos por que a aproximação se aplica. O erro na aproximação é de menos de 1 em 5000 se .

a. Com o seu software de gráfico no modo radiano, faça o gráfico de y = sen x e y = x juntos em uma janela de visualização em torno da origem. O que acontece à medida que x se aproxima da origem?

b. Com seu software de gráfico em modo graus, faça o gráfico de y = sen x e y = x juntos, novamente, em torno da origem. Qual a diferença entre a figura obtida aqui e aquela obtida no modo radiano?

Passo 1

O gráfico em radianos fica dessa forma:

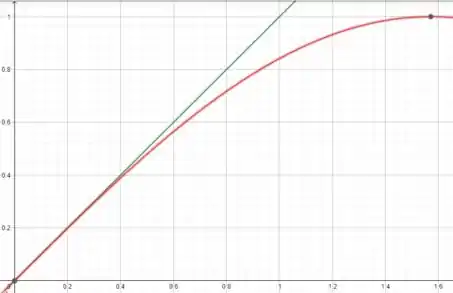
Quando se aproxima da origem ele fica cada vez mais parecido com

Passo 2

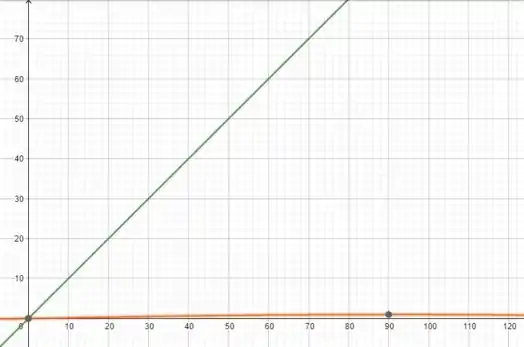
O gráfico com a calculadora em graus fica:

Quando se aproxima da origem ele está muito mais próximo de zero do que

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ⁡ ( t ) , s e c ⁡ ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da

Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ⁡ ( t ) , s e c ⁡ ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da

Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ⁡ ( t ) , s e c ⁡ ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da

Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ⁡ ( t ) , s e c ⁡ ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da

Use a periodicidade da função seno, cosseno, secante e cossecante, bem como os valores do s e n t , c o s ⁡ ( t ) , s e c ⁡ ( t ) e c o s e c ( t ) , quando 0 ≤ t2 π , para determinar o valor exato da