Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.7 - Ex. 2
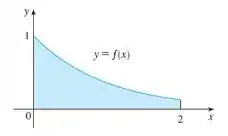
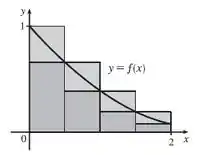
As aproximações pela extremidade esquerda, extremidade direita, Trapézio e Ponto Médio foram usadas para estimar , onde é uma função cujo gráfico é mostrado. As estimativas foram , , e e o mesmo número de subintervalos foi usado em cada caso.
- Qual regra produz qual estimativa?
- Entre quais aproximações está o valor verdadeiro de ?
Passo 1
- Temos, pelo diagrama abaixo, que , assim temos que:
- Como temos que , então o valor verdadeiro de está entre e .
, , e
Passo 2
Resposta
- , , e
- O valor verdadeiro de está entre e
Exercícios de Livros Relacionados
Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme inficado. Para cada exercício, faça uma figura mostrando a
Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme inficado. Para cada exercício, faça uma figura mostrando a
Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme inficado. Para cada exercício, faça uma figura mostrando a
Nos Exercícios de 21 a 36, use o método desta secção para calcular a área da região dada; use retângulos inscritos ou circunscritos, conforme inficado. Para cada exercício, faça uma figura mostrando a
Nos exercícios de 39 a 44, ache a área da região, tomando como medida da altura do i - é s i m o é retângulof ( m i ) , onde m i é o ponto médio do i - é s i m o é subintervalo. Sugestão: m i = 1 2 x