Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.10 - Ex. 22

Aproxime a integral definida pela regra de Simpson com o valor indicado de n. Expresse o resultado com três casas decimais.

∫ - 1 2 0 d x 1 - x 2

Com n = 4.

Passo 1

Essa questão tem um número relativamente grande de passos, porém tem como sintetizar a maioria deles em uma tabela, e nós do Responde AÍ recomendamos que você faça assim na sua prova pois fica mais organizado e mais fácil de se obter o resultado. Então bora lá:

Primeira coisa a se fazer é conhecer a fórmula usada para responde essa questão que será essa:

∫ a b f x d x = b - a 3 n [ f x 0 + 4 f x 1 + 2 f x 2 + … + 2 f x n - 2 + 4 f x n - 1 + f ( x n ) ]

Onde:

b = l i m i t e   s u p e r i o r   d a   i n t e g r a l

a = l i m i t e   i n f e i o r   d a   i n t e g r a l

n = n ú m e r o   d e   p a s s o s

f x = f u n ç ã o   a p l i c a d a   n o   p o n t o   x   e s s a   f u n ç ã o   é   a   f u n ç ã o   d a   i n t e g r a l .

Bastante atenção nos índices do f ( x ) .

Vamos entender agora exatamente como vai funcionar essa coisa feia aí.

Passo 2

Agora vamos encontrar o valor que multiplica tudo:

b - a 3 n = 0 - ( - 1 2 ) 3 * 4 = 1 24

Passo 3

Vamos encontrar quantos f x   terão nossa solução. No problema dar as informações necessárias que são: n = 4 e os intervalos de integração.

Se encontra dessa forma:

b - a n = 0 - ( - 1 2 ) 4 = 1   8

Ou seja, terão f ( x ) igualmente espaçados em 1 8   ,   começando no limite inferior ( a ) do nosso problema que no caso é ( - 1 2 ) .

Passo 4

Nesse passo é o que eu falei de sintetizar os passos. Construímos uma tabela no modelo que o livro fornece pra solucionar, logo:

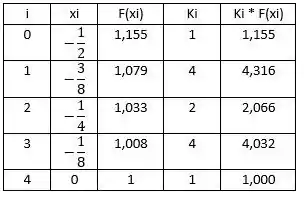
Onde os k i são os índices que acompanhar os f ( x ) na equação do passo 1. E os f ( x i ) é a própria função f ( x ) aplicada nos pontos x i . Nesse caso f x =   1 1 - x 2  

Passo 5

Agora basta apenas aplicar a forma direto:

∫ - 1 2 0 d x 1 - x 2 = 1 24 [ 1,155 + 4,316 + 2,066 + 4,032 + 1,000 ]

∫ - 1 2 0 d x 1 - x 2 = 1 24 [ 12,569 ]

∫ - 1 2 0 d x 1 - x 2 = 0,524

Chegamos ao fim da nossa jornada.

Resposta

∫ - 1 2 0 d x 1 - x 2 = 0,524

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a regra de Simpson para aproximar o valor médio da temperatura da função f x = 37s e n 27 365 x - 101 + 25 Para um ano de 365 dias. Essa é uma forma de estimar a temperatura média anual do ar em F
O calor especifico de um gás C é a quantidade de calor necessária para elevar a temperatura em 1° C de determinada massa de gás com volume constante, medida em Cal/°C-mol (calorias por grau centígrado
U se a regra do Trapézio para fazer uma aproximação do consumo de combustível total durante aquela hora. Se o automóvel fez 60 milhas nessa hora, qual foi a eficiência do combustível (em milhas por ga
De acordo com a fórmula que limita o erro para a regra de Simpson, quantos subintervalos você deve usar área estimar o valor de l n 3 = ∫ 1 1 1 xd x Pela regra de Simpson com um erro de não mais que 1
Você planeja usar a regra de Simpson para estimar o valor da integral ∫ 1 2f x d x Com uma magnitude de erro inferior a 10 - 5 . Você determinou que f 4 x ≤ 3 ao longo do intervalo de integração . Qua