Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.Revisão - Ex. 41

Aproxime a integral usando (a) a aproximação pelo ponto médio M 10 , (b) a aproximação trapezoidal T 10 e (c) a aproximação S 20 pela regra de Simpson. Em cada caso, encontre o valor exato da integral e aproxime o erro absoluto. Expresse sua resposta com pelo menos quatro casas decimais.

∫ 1 3 1 x + 1 d x

Passo 1

Vamos começar fazendo a aproximação pelo ponto médio. Calculamos o ∆ x :

∆ x = 3 - 1 10 = 0 , 2

Calculando a aproximação:

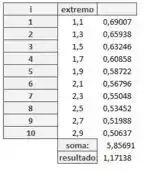
Achando os pontos multiplicamos o valor da soma pelo ∆ x :

∫ 1 3 1 x + 1 d x = 0,2 × 5,85691

Assim, temos que a aproximação pelo ponto médio é M 10 ≈ 1,17 1 38 . O valor aproximado da integral é ∫ 1 3 1 x + 1 d x ≈ 1.17157 , assim, o erro será

E M = 1.17157 - 1,17138 = 0,00019 0169

Passo 2

Para a aproximação trapezoidal, temos:

∆ x = 3 - 1 2 × 10 = 0 , 1

Calculando a aproximação:

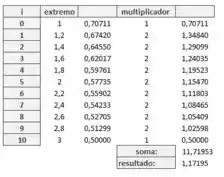
Achando os pontos multiplicamos o valor da soma pelo ∆ x :

∫ 1 3 1 x + 1 d x = 0 , 1 × 11,71953

Assim, temos que a aproximação trapezoidal é T 10 ≈ 1,17 195 . O valor aproximado da integral é ∫ 1 3 1 x + 1 d x ≈ 1.17157 , assim, o erro será

E T = 1.17157 - 1,17195 = 0,00038 0588

Passo 3

E por fim, para a regra de Simpson, temos:

∆ x = 1 3 × 3 - 1 2 0 = 1 30

Calculando a aproximação:

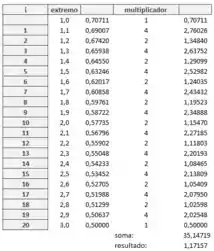
Achando os pontos multiplicamos o valor da soma pelo ∆ x :

∫ 1 3 1 x + 1 d x = 1 30 × 35,14719

Assim, temos que a aproximação trapezoidal é S 2 0 ≈ 1,171 57 . O valor aproximado da integral é ∫ 1 3 1 x + 1 d x ≈ 1.17157 , assim, o erro será

E S = 1 , 17157 - 1,171 57 = 8,35151 × 10 - 8

Prontinho!!

Resposta

M 10 ≈ 1,17138 e E M = 0,00019 0169

T 10 ≈ 1,17195 e E T = 0,00038 0588

S 20 ≈ 1,17157 e E S = 8,35151 × 10 - 8

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A figura a seguir mostra a curva a aceleração versus tempo de uma partícula que se move ao longo de um eixo. Se a velocidade inicial da partícula for de 20m / s , estime ( a ) a velocidade no instante
A figura a seguir mostra a curva a aceleração versus tempo de uma partícula que se move ao longo de um eixo. Se a velocidade inicial da partícula for de 20m / s , estime ( a ) a velocidade no instante
Em cada parte, é dada a curva velocidade versus tempo de uma partícula que se move ao longo de uma reta. Use a curva para encontrar o deslocamento e a distância percorrida pela partícula no intervalo
Nestes exercícios, suponha que o objeto move-se com aceleração constante no sentido positivo de um eixo. Aplique as Fórmulas (10) e (11) conforme for apropriado. Em alguns dos problemas, você necessit
Nestes exercícios, suponha que o objeto move-se com aceleração constante no sentido positivo de um eixo. Aplique as Fórmulas (10) e (11) conforme for apropriado. Em alguns dos problemas, você necessit