Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 7.7 - Ex. 26

Aproxime a integral usando a regra de Simpson S 10 e compare sua resposta com aquela produzida por algum recurso computacional provido de integração numérica. Expresse suas respostas com pelo menos quatro casas decimais.

∫ 0 3 x 2 x 3 + 1 d x

Passo 1

E aíííí, galerinha! Prontos pra mais um exercício com o Responde Aí?

Bom, para esse exercício em questão, a ideia é bem simples. Vamos resolver da maneira mais trivial: apenas calculando a integral aplicando a fórmula da regra citada.

Assim, lembrando que a fórmula da aproximação é dada por:

S n = 1 3 b - a n y 0 + 4 y 1 + y 3 + … + y n - 1 + 2 y 2 + y 4 + … + y n - 2 + y n

Podemos montar uma tabela para cada valor de y nos n subintervalos a fim de facilitar o nosso trabalho.

Para esse caso temos os seguintes valores:

n = 10 ,   a = 0 ,   b = 3

Ainda, o software usado para calcular a integral será o WolframAlpha e o resultado obtido será comparado ao encontrado na regra em questão.

Passo 2

Então, para a nossa respectiva integral

∫ 0 3 x 2 x 3 + 1 d x

Temos que y = f x = x 2 x 3 + 1 . Então, podemos montar a seguinte tabela:

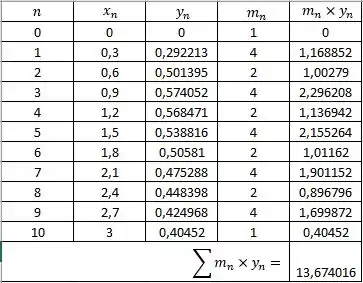
Então, a aproximação se dará por:

S 10 = 1 3 3 - 0 10 13,674016

Portanto:

S 10 = 1,367402

Passo 3

Agora, através do Software citado na explicação obtemos:

∫ 0 3 x 2 x 3 + 1 d x ≈ 1,36748

Observando os dois resultados, conseguimos ver que a regra de Simpson nos dá resultados praticamente exatos com um erro bem pequeno se comparado ao do software. Calculando o erro da nossa aproximação temos:

E S = 1,36748 - 1,367402 × 100 %

Então:

E S = 0,0078 %

Resposta

S 10 = 1,367402

∫ 0 3 x 2 x 3 + 1 d x ≈ 1,36748

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Expresse o limite como uma integral definida no intervalo dado. lim n → ∞ ⁡ ∑ i = 1 n e x i 1 + x i Δ x ,[ 1 ,5 ]
Calcule a soma de Riemann para f x = 2 - x 2 ,0 ≤ x ≤ 2 , com 4 subintervalos, tomando os pontos amostrais como os extremos direitos. Explique, com a ajuda de um diagrama, o que representa a soma de R
A tabela fornece os valores de uma função obtidos experimentalmente. Use-os para estimar ∫ 0 6 f x d x utilizando três subintervalos iguais com (a) extremos direitos, (b) extremos esquerdos e (c) pont
a) Ache a soma de Riemann para f x = x - 2 sen ⁡ 2 x ,0 ≤ x ≤ 3 , com seis termos, tomando como pontos amostrais os extremos direitos. (Dê sua resposta correta até a sexta casa decimal.) Explique o qu
Ache as aproximações T n , M n e S n para n = 6 e 12 . Então calcule os erros correspondentes E T , E M e E S . (Arredonde seus resultados para seis casas decimais. Você pode usar o comando soma em um