Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.2 - Ex. 72

72. Área Determine a área entre o eixo das abscissas e a curva 1 + cos ⁡ 4 x ,   0 ≤ x ≤ π

Passo 1

O exercício se refere a essa região

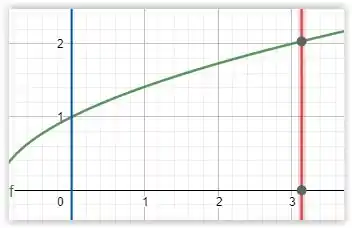
E temos que determinar a área.

Passo 2

Vamos lá, a área vai ser a integral da função 1 + cos ⁡ 4 x

A = ∫ 0 π   1 + cos ⁡ 4 x d x  

Podemos fazer a seguinte substituição

x = u 2 d x = d u 2

Então ficaremos com

∫ 0 π   1 + cos ⁡ 4 x d x   = 1 2 ∫ 0 π   1 + cos ⁡ 2 u d u  

Mas

cos ⁡ 2 u = - 1 + 2 c o s 2 u

Então a integral fica

1 2 ∫ 0 2 π   1 + cos ⁡ 2 u d u   = 1 2 ∫ 0 2 π   1 - 1 + 2 c o s 2 u d u =   2 2 ∫ 0 π 2   cos ⁡ u d u + ∫ π 2 3 2 π - cos ⁡ u   d u + ∫ 3 π 2 2 π cos ⁡ u   d u

Passo 3

Agora vamos calcular a integral

2 2 ∫ 0 π 2   cos ⁡ u d u + ∫ π 2 3 2 π - cos ⁡ u   d u + ∫ 3 π 2 2 π cos ⁡ u   d u = 2 2 s e n π 2 + s e n 3 2 π - s e n π 2 + s e n   2 π - s e n 3 2 π =   2 2 1 + 2 + 1 = 2 2

Resposta

2 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use as fórmulas de Wallis do Exercício 68 para calcular a ∫ 0 π 2 sin 3 ⁡ x d x b ∫ 0 π 2 sin 4 ⁡ x d x c ∫ 0 π 2 sin 5 ⁡ x d x d ∫ 0 π 2 sin 6 ⁡ x d x
Descreva as várias abordagens para calcular integrais da forma ∫ sin m ⁡ x ⋅ cos n ⁡ x d x Quais são os casos em que esses tipos de integrais se dividem? Quais são os procedimentos e as identidades us
( a ) Use a Fórmula ( 9 ) da Seção 7.2 para mostrar que ∫ 0 π 2 sin n ⁡ xd x = n - 1 n ∫ 0 π 2 sin n - 2 ⁡ x d x ( n ≥ 2 ) ( b ) Use esse resultado para deduzir as fórmulas de Wallis para o seno ∫ 0 π
Calcule a integral. ∫ s e nx cos ⁡ 2 x d x
Calcule a integral. ∫ s e n 25 θ d θ