(a) Dê um argumento geométrico para mostrar que 1 x + 1∫ x x + 1 1 t d t1 x , x0 (b) Use o resultado de (a) para provar que 1 x + 1ln ⁡ 1 + 1 x1 x , x0 (c) Use o resultado de (b) para provar que e x / ( x + 1 )1 + 1 x xe , x0 e, portanto, que lim x → ∞ ⁡ 1 + 1 x x = e (d) Use o resultado em (b) para provar que 1 + 1 x xe1 + 1 x x + 1 , x0

Enunciado

(a) Vamos refletir. A gente tem que:

E essa integral do meio calcula a área embaixo da curva entre esses valores de . Vamos colocar isso num gráfico:

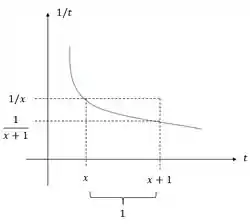
A área que a gente quer achar está entre e , e abaixo dessa curva azul. Repara que essa área é menor do que o retângulo de área:

Mas é maior do que o retângulo de área:

Colocando isso numa inequação:

E isso é exatamente o que precisávamos provar!

(b) Vamos calcular a integral do meio da inequação:

Lembrando das propriedades de log:

Substituindo isso na inequação:

Podemos aplicar a função exponencial natural em todos os termos:

Depois elevar todos os termos a e usar propriedade de potência:

Vamos aplicar o limite de em todos os termos:

Resolvendo o da direita separadamente:

Se substituirmos , ele vai dar uma indeterminação . Podemos usar L’Hospital:

Voltando para as continhas de cima:

E a nossa inequação fica:

Pelo Teorema do Confronto, a gente tem que:

(d) Na letra (c) a gente já tinha saído de (b) e chegado em

Daí a gente já tem que:

Vamos agora trabalhar com:

Podemos elevar os dois lados a e usar propriedade de potência:

Juntando as duas inequações:

Prova nos passos