Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 33
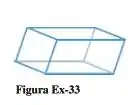
Uma armação em arame consiste em dois quadrados idênticos, cujos vértices estão ligados por quatro fios restos de mesmo comprimento (Figura Ex-33 a seguir). Se a armação for feita com um único fio de arame de comprimento , quais devem ser as dimensões para obter uma caixa com o maior volume?
Passo 1
Então pessoal, antes de começarmos a resolução vamos definir quem são nossas variáveis, ok? Vamos chamar de o comprimento dos quadrados e a altura dos mesmos. Sendo assim, podemos definir o volume como:
Que é o produto entre a área da base e a altura. Além disso, temos que o comprimento do arame é:
Isolando nessa expressão:
Substituindo em , teremos:
Show!
Passo 2
Como queremos descobrir as dimensões para obter um volume máximo, devemos utilizar os conceitos de máximo e mínimo, assim como estudamos na seção em questão! Derivando nossa função, teremos:
Igualando nossa derivada a zero:
Agora que encontramos a primeira dimensão, para encontrarmos a segunda basta substituirmos esse valor que acabamos de achar, se liga:
E está aí nossa resolução, galera! 😉