Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.9 - Ex. 36

Use o método de Newton para encontrar o valor mínimo absoluto da função f x = x 2 + sen ⁡ x correto até a quarta casa decimal.

Passo 1

Os pontos críticos da função ocorrerão quando sua derivada for zero. Derivando f ( x ) , temos:

f ' x = 2 x + cos ⁡ x

Devemos então usar o método de Newton para encontrar as raízes de f ' ( x ) .

Usando o método de Newton, as aproximações são dadas pela fórmula:

x n + 1 = x n - g x n g ' x n

Temos:

g x = f ' x = 2 x + cos ⁡ x

g ' x = f ' ' x = 2 - sen ⁡ x

Então a fórmula fica:

x n + 1 = x n - 2 x n + cos ⁡ x n 2 - sen ⁡ x n

Agora basta escolher uma aproximação inicial adequada, e então aplicar a fórmula até os resultados não diferirem na quarta casa decimal.

Passo 2

Devemos ter 2 x + cos ⁡ x = 0 ⇒ - 2 x = cos ⁡ x , então esboçamos os gráficos de - 2 x e cos ⁡ x para estimar onde está a raiz:

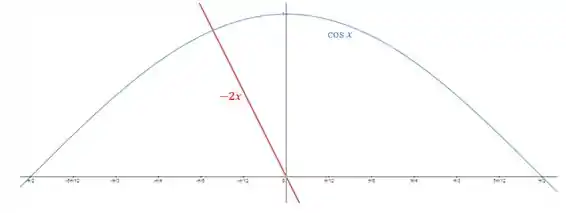
Podemos ver que o valor está próximo de - π 6 ≈ - 0,523 . Vamos começar com o chute inicial de x 1 = - 0,5 .

Passo 3

Vamos então aplicar o método de Newton:

x 1 = - 0.5

x 2 = - 0.5 - 2 - 0.5 + cos ⁡ - 0.5 2 - - 0.5 = - 0.451033

x 3 = - 0.451033 - 2 - 0.451033 + cos ⁡ - 0.451033 2 - - 0.451033 = - 0.450188

x 4 = - 0.450188 - 2 - 0.450188 + cos ⁡ - 0.450188 2 - - 0.450188 = - 0.450183

Como x 3 e x 4 são iguais até a quarta casa decimal, temos x = - 0,4501 .

Passo 4

Como a função f x = x 2 + sen ⁡ x é muito grande para x muito pequeno ou x muito grande, o único ponto crítico tem que ser obrigatoriamente o mínimo absoluto. Então:

f m í n = f - 0,4501 = - 0,4501 2 + sen ⁡ - 0,4501 = - 0,2324

Resposta

f m í n = - 0,2324

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

51-60 Dê um gráfico de polinômio e identifique as coordenadas dos cortes com os eixos, dos pontos estacionários e dos pontos de inflexão. Confira as respostas com um recurso gráfico.52- p x = 1 + 8 x
37-50 Use qualquer método para encontrar os extremos da função f .49- f x = 3 x - x 2
51-60 Dê um gráfico de polinômio e identifique as coordenadas dos cortes com os eixos, dos pontos estacionários e dos pontos de inflexão. Confira as respostas com um recurso gráfico.54- p x = 2 - x +
Um retângulo tem dois cantos inferiores no eixo x e dois cantos superiores na curva y = 16 - x 2 . Dentre todos esses retângulos, quais as dimensões daquele que tem maior área.
Uma caixa de base quadrada é mais alta do que larga. Para poder mandá-la pelo correio dos EUA, sua altura e o perímetro da base devem somar não mais que 108 polegadas. Qual é o volume máximo dessa cai