Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.9 - Ex. 34
(a)Se , encontre
(b) Verifique se sua resposta em (a) foi razoável e comparando os gráficos de e
Passo 1
E aí, meus amores, tudo certinho?
Aqui a gente quer calcular a derivada da função:
E depois usar o seu gráfico da sua derivada pra ver se a resposta que calculamos faz sentido.
Bem, primeira coisa é derivar então ne. E pra isso, vamos usar a fórmula da definição da derivada:
Então olha bem nessa fórmula o que temos e o que não temos. Só não temos ne, então ele é a primeira coisa que vamos calcular.
Passo 2
Temos:
Pra calcular , precisamos substituir em todos os lugares em que aparece na função. E fica assim:
Agora, esse termo ao quadrado ali no denominador, como você acha que a gente pode abrir ele? Ele é o quadrado de uma soma ne? Então vamos lembrar daquele produto notável
No nosso termo fica
Uhuull! Substituindo aqui:
E agora sim, vamos substituir no limite:
Ufa! Vamos pro passo 3 calcular esse limite!
Passo 3
Igualando os denominadores das frações do numerador:
Arrumando o denominador:
Fazendo a distributiva no numerador:
Agora vamos cortar os termos iguais:
Fatorando o numerador:
Cortando do numerador com o denominador:
Agora finalmente, vamos calcular o limite:
Uhuuullll, achamos a derivada da nossa função!
Passo 4
Nesse passo, faremos a análise gráfica de e .
Como são funções mais complexas, vamos usar um software pra encontrar seus gráficos.
Gráfico de
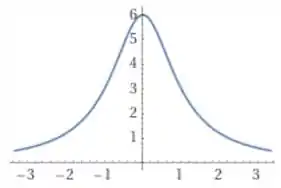
Gráfico de
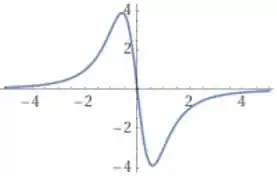
Repara só essas 3 características nos nossos gráficos:
- Quando a função é crescente, sua derivada é positiva
- Quando a função é decrescente, a derivada é negativa
- Quando a função atinge um máximo , ela tem tangente horizontal e a derivada é nula
É exatamente esse o comportamento que esperamos encontrar! Aliais, leva esses 3 tópicos que eu listei agora com você pra sua vida ;D
Resposta
Os gráficos confirmam esse resultado!