Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.5 - Ex. 37
Use o roteiro desta seção para esboçar a curva
Passo 1
Oi meus queridos, tudo certo com vocês?
Aqui nós temos a função
E aqui vamos seguir o seguinte roteiro para esboçar o gráfico dela.
A. Encontrar o domínio em que a função é definida.
B. Encontrar os interceptos. Que são os pontos onde a função cruza o eixo , isso é:
E o pontos onde a função cruza o eixo , isso é:
C. Verificar se há simetria par, isso é:
Para isso, basta substituir por e verificar se a expressão se mantém a mesma.
D. Procurar por assíntotas horizontais e verticais.
Uma assíntota horizontal é um valor real para o qual a função tende quando tende para infinito:
Já uma assíntota vertical é um valor de no qual a função possui uma descontinuidade e tende para infinito.
E. Encontrar os intervalos de crescimento e decrescimento. Para isso, basta derivar a função e nos intervalos em que a derivada for positiva a função cresce
E nos intervalos em que a derivada for negativa a função decresce
F. Encontrar os pontos de máximo e mínimo local.
Esses pontos ocorrem quando a derivada vale zero e troca de sinal ou quando a derivada possui uma descontinuidade e troca de sinal.
Caso a derivada fosse negativa e depois do ponto ela é positiva, então a função possui um ponto de mínimo local. Se a derivada era positiva e depois do ponto ela é negativa, então a função possui um ponto de máximo local.
G. Encontrar os intervalos de concavidade e pontos de inflexão.
A concavidade é para cima se a derivada segunda for positiva
E a concavidade é para baixo se a derivada segunda for negativa
Por fim, um ponto de inflexão é um ponto onde a derivada segunda vale zero e troca de sinal.
H. Esboçar a função juntando as informações obtidas.
Passo 2
Pra começar, vamos encontrar o domínio da função.
Repare que não temos nenhuma restrição. Assim, o domínio da nossa função será .
Agora vamos ver os pontos de interseção com os eixos.
Se :
Se
Como :
Logo,
Ou
Assim,
Portanto, nossa curva cruza o eixo nos pontos .
Passo 3
Para analisarmos a simetria, é importante vermos se nossa função é ímpar, par ou se não possui paridade. Então vem comigo!
Vamos ver como fica o :
Como o seno é uma função ímpar:
Com isso, vemos que . Portanto, nossa função será ímpar o que nos leva a concluir que a curva será simétrica com relação ao eixo .
Passo 4
Seguindo o roteiro, chegamos à tarefa de analisar as assíntotas.
- Assíntota horizontal
Da trigonometria:
Logo,
Somando com :
Pelo Teorema do Sanduiche concluímos que o limite não existe, pois nossa função fica oscilando entre os valores e . Portanto, não haverá assíntotas horizontais.
A gente também pode simplesmente falar que essas funções são funções periódicas e que portanto não possuem limite quando o seu argumento tende a infinito.
Não haverá assíntotas verticais, pois a função é definida em todo o conjunto dos reais, logo não apresenta descontinuidades.
Passo 5
Para acharmos os intervalos de crescimento e decrescimento, temos que achar .
Derivando,
Como :
Fatorando:
Para :
Resolvendo a inequação:
Logo, nossa curva será crescente no intervalo acima.
Para :
Resolvendo a inequação:
Então nossa curva será decrescente no intervalo acima.
Passo 6
Agora temos que achar os valores máximo e mínimos. Para isso, vamos fazer :
Logo,
Então podemos ter ou .
Se :
Se :
Ou
Passo 7
Para acharmos a concavidade da curva vamos analisar seu crescimento e decrescimento. Vem comigo!
Como a curva cresce de até e decresce até o . Isso significa que em teremos um ponto de máximo, portanto, concavidade para baixo no intervalo . O mesmo ocorre para todos os valores da forma .
Outra coisa que sabemos é que a curva é decresce de até e começa a crescer até . Isso quer dizer que teremos um ponto de mínimo, portanto, concavidade para baixo no intervalo . O mesmo irá ocorrer para valores da forma .
Passo 8
Pra finalizar, basta esboçarmos o gráfico de :
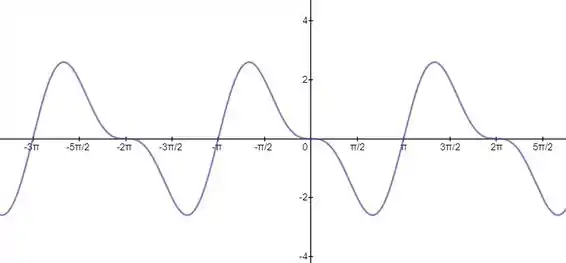
Resposta
