Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.2 - Ex. 6
O que todos os membros da família de funções lineares
têm em comum? Esboce os gráficos de vários membros da família.
Passo 1
Fala aí! tudo certinho? 👀
Nesse problema queremos determinar o que todos os membros da família de funções lineares
têm em comum e esboçar os gráficos de vários membros dessa família. Para isso, vamos revisar sobre a equação de uma reta, e o significado de alguns pontos.
A equação geral da reta pode ser dada por:
Em que é o coeficiente angular da reta, ele que diz qual a inclinação para a reta, e para casos em que temos que a reta é crescente e para casos a reta é decrescente.
Já , representa o coeficiente linear da reta, e é onde a reta toca o eixo . Para resolvermos essa atividade, iremos desenvolver a função, até que tenhamos uma reta parecida com a geral, e iremos gerar o gráfico dela utilizando o GeoGebra, a partir daí poderemos ver o que essa família tem de comum.
Vamos lá!
Passo 2
Temos uma questão investigativa! O enunciado nos dá uma função linear geral , onde pode assumir qualquer valor. Então poderíamos ter:
E por ai vai, podemos ter infinitas funções... mas o que todas elas vão ter em comum?!
Como temos uma função linear, podemos reescrever na forma da equação da reta.
Abrindo a função e reorganizando-a:
Temos então:
Tranquilo até aqui? 😁
Passo 3
Escolhendo alguns valores para podemos desenhar algumas retas pertencentes a família da função. Basta escolhermos valores para e , que teremos diferentes retas em diferentes pontos.
Pra isso vamos fazer uma tabelinha:
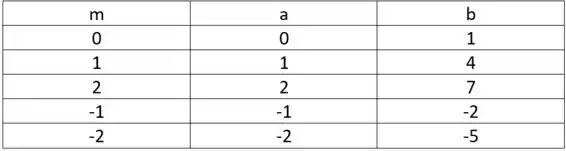
Com os valores diferentes para , teremos então as funções:
Na figura abaixo iremos plotar com ajuda do GeoGebra algumas retas com os seus respectivos valores de .
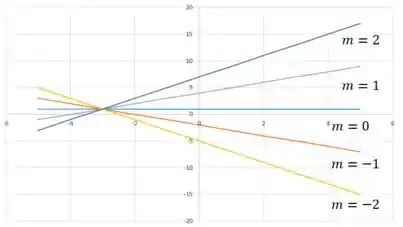
Repare no gráfico que todas as retas se encontram em um determinado ponto (). Isto é o que todos os membros da família de funções lineares do tipo
têm em comum.
E aí! entendeu tudo? Responde Aí! 😉
Resposta
Todas as retas correspondentes aos membro dessa família se encontram no ponto: