Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 54
Associe as curvas polares com seus respectivos gráficos . Dê razões para suas escolhas. (Não use uma ferramenta gráfica.)
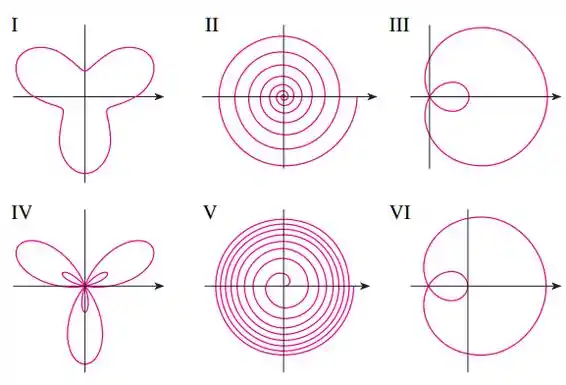
Passo 1
Nessa questão vamos analisar cada equação, prever o comportamento de sua curva para relacionarmos com as imagens de .
Precisamos aqui analisar cada função. O que a gente vai fazer é entender como as funções variam quando mudamos os valores de . Iremos também analisar pontos importantes do gráfico, raízes, pontos de interseção.
Passo 2
Se analisarmos a equação, à medida que aumenta o também aumenta, mas cada vez mais a uma taxa menor. Então essa curva vai ter um formato espiralado, mas como a taxa de variação vai diminuindo, cada vez mais a diferencia de distância de um ciclo anterior ( de diferença) é menor.
Temos 2 curvas espirais, a e a , mas a que segue o que analisamos é a curva pois o que diferencia as duas, é a ‘velocidade’ que as voltar acontecem. A isso acontece com uma frequência menor, já que temos aqui uma raiz.
Analisando essa equação, assim como na primeira vai ter um formato espiralado, mas diferente da anterior, a taxa de variação aumenta ao aumentar o , portanto a diferença de valor da função pra um cilo anterior vai aumentando.
A curva que representa esse comportamento é a .
Passo 3
Para essa curva vamos analisar a função para alguns valores de
Para chegarmos a curva que está representada precisaríamos de mais um ciclo, porém só com esses valores já é possível chegar a conclusão de que a curva que essa equação gera é a .
Passo 4
Calculando alguns valores da função:
Das curvas restantes, a que tem o comportamento que segue esses valores nos eixos é a curva .
Passo 5
Calculando alguns valores da função:
Pelos valores da função, analisando as curvas restantes, a que representa a equação é a .
Passo 6
Só sobrou uma curva, então se estiver tudo certo a curva que representa essa equaç��o é a Mas vamos analisar tudo certinho, primeiro calculando a função em alguns pontos:
Para uma melhor analise seria importante nós vermos como a função se comporta entre esses valores, mas pelas 6 curvas que temos, a que se encaixa nesses valores calculados é de fato a curva .