Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.1 - Ex. 9
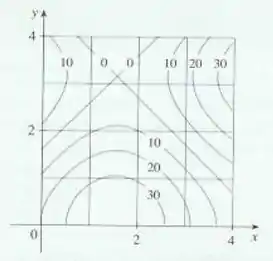
A figura mostra o mapa de contorno de no quadrado .
- Use a Regra do Ponto Médio com para estimar o valor de .
- Estime o valor médio de .
Passo 1
E aí futuro cientista, preparado para usar todo seu talento em cálculo nessa questão de matemática? Vamos arrebentar!
Claro, aqui está a resolução atualizada com os passos explicitados em forma de texto:
Primeiramente, determinamos a área total da região , que é o quadrado com lados de comprimento . Ao dividir essa área em sub-retângulos de igual tamanho, calculamos a área de cada sub-retângulo, o que nos dá . Em seguida, calculamos os pontos médios de cada sub-retângulo, que são os pontos onde a função será avaliada.
Vamos usar a Regra do Ponto Médio para estimar a integral , onde . Para isso, precisamos calcular , que é a área de cada sub-região.
Passo 2
(a) Usando a regra do ponto médio temos que os pontos do intervalo utilizado vão ser o ponto médio de cada intervalo, e temos que , para calcular a integral precisamos calcular quem é .
Temos que a área total da região vista no mapa é:
Então vai ser:
Pronto, agora vamos usar a soma de Riemann para estimar a integral:
Lembrando que são os pontos médios de cada intervalo:
Pronto, o valor estimado da integral é .
Passo 3
(b) Temos que para estimar o valor médio de usamos a expressão:
Já temos o valor de que é igual a , que foi calculado no passo anterior, e acabamos de calcular a integral, então é só substituir os valores: