Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.1 - Ex. 9
Os Exercícios 1-18 fornecem equações paramétricas e intervalos de parâmetro para o movimento de uma partícula no plano xy. Identifique a trajetória da partícula encontrando a equação cartesiana para ela. Desenhe o gráfico de cartesiana (os gráficos irão variar confor-
me a equação utilizada). Indique a parte do gráfico percorrida pela partícula e a direção do movimento.
Passo 1
Opa! E aí, tudo bem?! O enunciado nos deu as seguintes equações paramétricas:
Para o intervalo:
Essas equações representam a trajetória de uma partícula no plano .
O que a gente precisa fazer aqui é “desparametrizar” essas curvas, ou seja. Agora a gente tem e em função de e precisamos encontrar em função de , sacou?!
Depois disso a gente vai esboçar o gráfico da função que representa a trajetória da partícula!
Não precisa se assustar com as equações parametrizadas! A gente vai usar identidades trigonométricas pra sair desse problema!
Passo 2
A gente tem que:
Queremos escrever em função de e temos um arco duplo! Huuum...acho que essa identidade aqui pode nos ajudar:
Então podemos dizer que:
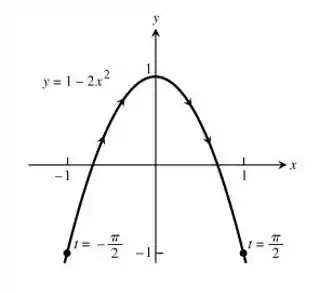
A trajetória da nossa partícula é uma parábola com concavidade pra baixo!
Passo 3
Agora precisamos achar o nosso intervalo! Lembrando que:
Pra descobrir nosso intervalo em função de só precisamos substituir as extremidades em:
Substituindo:
Assim:
Agora é só esboçar a nossa parábola:
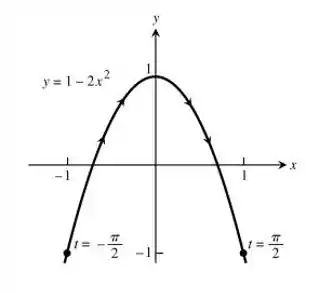
Resposta
