Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 52
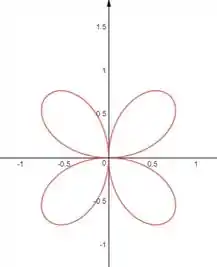
Esboce a curva
Passo 1
Essa equação não tem uma cara muito bonita e não parece algo familiar, que reconheceríamos simplesmente no plano.
A maneira mais simples de esboçar essa curva seria por mudança de variável, no caso vamos mudar para coordenadas polares.
Passo 2
Fazendo a mudança de variáveis usaremos
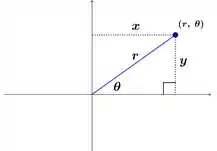
Fazendo a decomposição do vetor e em termos de .
Substituindo tudo na nossa equação teremos
Passo 3
Sabemos
Distribuindo os expoentes dentro dos parênteses
Fazendo a multiplicação entre as potências semelhantes.
Dividindo a equação por
Temos então
Podemos agora usar a relação trigonométrica: . Se elevarmos essa relação ao quadrado teremos que: . Substituindo na equação:
Aplicando a raiz quadrada em ambos os lados temos
Passo 4
Agora para esboçar o gráfico desta equação valor calcular alguns valores da função, do 1° ao 4 quadrante.
Para :
Para
1° Quadrante: O argumento do seno vai variar de a , por conta do multiplicativo dentro do argumento. O valor do seno nesse intervalo varia de a e depois retorna ao .
Passo 5
Para
No 2° Quadrante o segundo quadrante o argumento vai variar de até e o valor do seno vai de a e retorna ao .
Passo 6
Para
Para o terceiro quadrante o comportamento vai ser igual ao do primeiro, pois o argumento vai variar de até , e neste intervalo o seno tem valor igual ao do intervalo de a
Passo 7
Para
Pela mesma lógica no quarto quadrante o comportamento será igual ao do segundo quadrante.
Passo 8
Representação do gráfico:
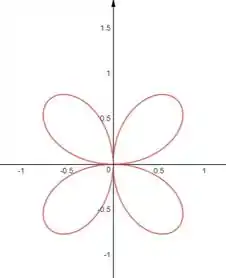
Resposta
