Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.3 - Ex. 45
Esboce uma curva com a equação polar dada primeiro esboçando o gráfico de como função de em coordenadas cartesianas.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte equação polar:
Queremos esboçar a sua curva polar.
Mas antes temos que esboçar a curva em coordenadas cartesianas.
Assim, para montar essa primeira curva, podemos comparar a função que nos foi dada com uma função parecida que já sabemos como se plota.
Em seguida, vamos analisar como o valor de varia a cada (em cada quadrante) para podermos plotar a curva polar.
É sempre bom relembrar que nas equações polares o representa a distância do ponto até a origem e o o ângulo do ponto em relação ao eixo horizontal positivo.
Passo 2
Vamos analisar a nossa função:
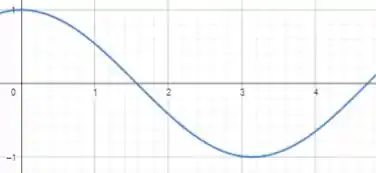
A gente pode partir da curva , né? Essa a gente sabe que é dada da seguinte forma:
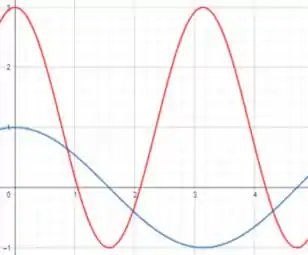
Comparando as expressões, vemos na equação do enunciado:
- Temos a soma : isso significa que nosso gráfico “sobe” em uma unidade;
- Temos o argumento : isso significa que nossa curva é “comprimida” em uma proporção de duas vezes;
- Temos um multiplicando o cosseno: isso significa que a amplitude do nosso gráfico dobra.
Assim, com essas informações, temos a curva em vermelho:
Passo 3
Para plotarmos na forma polar, primeiramente vamos calcular valores de para alguns valores de (você pode conferir com os valores do gráfico do passo anterior também 😉).
Vamos calcular para e (ou seja, uma volta completa).
Primeiramente para :
Assim, o do nosso gráfico começará e em .
Passo 4
Para , temos:
Assim, no primeiro quadrante a gente começa com e finaliza com .
Passo 5
Para , temos:
Assim, no segundo quadrante a gente começa com e finaliza com .
Passo 6
Para , temos:
Assim, no terceiro quadrante a gente começa com e finaliza com .
Passo 7
Para , temos:
Assim, no quarto quadrante a gente começa com e finaliza com .
Passo 8
Com base no que descrevemos nos passos anteriores, ao analisar cada quadrante, temos a seguinte curva:
Resposta
