Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.7 - Ex. 30

Use o Método de Newton para aproximar o máximo absoluto de f x = 1 - 2 x a r c t g   x .

Passo 1

Fala aí! Tudo joia?

Máximo absoluto ocorre onde a derivada é zero, certo? Vamos começar derivando essa função então...

f ' x =   - 2   a r c t g   x + 1 - 2 x 1 + x 2

A gente precisa dos pontos onde essa derivada é zero.

- 2   a r c t g   x + 1 - 2 x 1 + x 2 = 0

Passo 2

Vamos ver o gráfico da função f pra a gente ter uma noção:

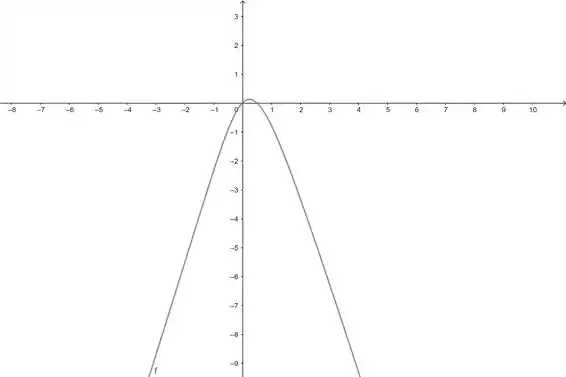
Pelo gráfico a gente vê que o ponto máximo tá ali próximo de x = 0,5 . Vamos fazer uma aproximação mais legalzinha com o método de Newton!

Passo 3

Para usar o método de Newton, a gente faz:

x n + 1 = x n - g x n g ' x n

Sendo o nosso x 1 = 0,5 e g x = - 2   a r c t g   x + 1 - 2 x 1 + x 2   e g ' x = - 4 + 2 x 1 + x 2 2

Aí a gente joga na fórmula:

x 2 = 0,5 - - 2 a r c t g   0,5 + 1 - 2 0,5 1 + 0,5 2 - 4 - 2 0,5 1 + 0,5 2 2 = 0,21

x 3 = 0,24

x 4 = 0,25

Pronto, vamos parar por aqui. O ponto de máximo absoluto está aproxidamente em x = 0,25 .

Passo 4

Agora pra encerrar, é só a gente ver o valor máximo da função. Só fazer:

f 0,25 =   0,12

Prontinho! Esse é o máximo absoluto da função😉

Resposta

Pontos máximo: ( 0,25 ,   0,12 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine os pontos críticos da função y = x 2 - 32x
Determine os pontos críticos da função f x = x ² x - 2 ²
Determine os valores extremos (absoluto e local) das funções e onde ocorrem: y = x ³ ( x - 5 ) ² ³ ²
Determine os valores extremos (absoluto e local) das funções e onde ocorrem: y =3 + 2 x - x 2
Determine os valores extremos (absoluto e local) das funções e onde ocorrem: y = x + 1 x 2 + 2 x + 2