Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.1 - Ex. 21
Descreva o movimento de uma partícula com posição quando varia no intervalo dado
Passo 1
Olá, meu amigo. Vou te ajudar a resolver essa atividade.
Vamos descobrir como lemos funções no formato paramétrico.
Nossas equações são:
E uma forma de encontrarmos o movimento da nossa partícula é criarmos uma tabela para diferentes valores de e seus respectivos valores para e .
Ao criarmos nossa tabela, deveremos nos atentar para o intervalo de , que é:
Após criarmos nossa tabela, iremos colocar os pontos no plano cartesiano utilizando um software gráfico, estarei utilizando o GeoGebra, você pode utilizar um da sua preferência. Com os pontos em mão, conseguiremos entender o comportamento da curva.
Passo 2
Criando então a nossa tabela de valores, temos:
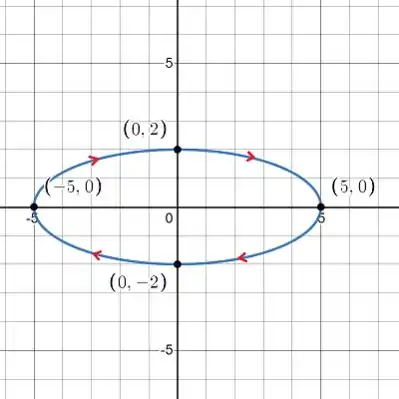
A partícula, descrita por equações paramétricas, se move ao longo da curva na direção das setas conforme aumenta. Vemos que ela começa no ponto e termina no ponto . A partícula percorre a curva vezes.
A partícula continua se movendo ao longo da elipse no sentido horário. Completa a primeira revolução em Completa a segunda revolução em . Completa a terceira revolução em .
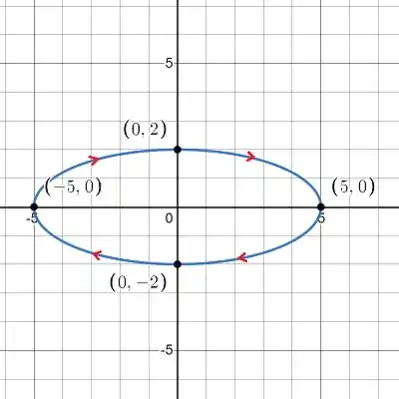
No nosso gráfico você pode acompanhar o movimento da partícula. Mas essa forma de resolver não é a única forma, a gente pode também voltar a equação paramétrica para a forma cartesiana, e assim encontrarmos uma equação conhecida. Vamos fazer isso.
Passo 3
Então, nos é dado:
Podemos reescrever como:
Vamos então utilizar da identidade trigonométrica:
Podemos concluir que a partícula se move em uma elipse. Pois essa é uma equação da elipse.
Resposta
