Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.1 - Ex. 10
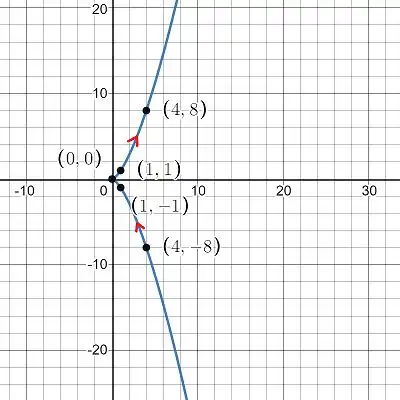
A ) Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando t aumenta
B ) Elimine os parâmetros para encontrar uma equação cartesiana da curva
Passo 1
Olá, meu amigo. Vamos resolver essa atividade juntos.
Esse é um exercício que te ajuda a criar gráficos. Algo muito importante, principalmente quando formos avançando e chegando por exemplo em cálculo 3.
Aqui a gente tem a curva parametrizada:
E precisamos esboçar seu gráfico marcando pontos. Isso é, iremos assumir alguns valores para e encontrar os seus respectivos valores em e .
Já para a letra b), iremos isolar o valor de em qualquer uma das equações, e após isso iremos substituir na outra equação, tendo assim uma equação dependente apenas de e .
Passo 2
Vamos fazer o seguinte, vamos criar uma tabela com valores de e plotar esses pontos num gráfico.
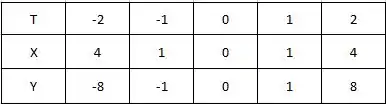
Beleza, tendo esses pontos. Vamos analisar eles. Observe que eles são simétricos, isso é Isso vai fazer nosso gráfico ficar espelhado. E como não tem valores negativos, vamos ver apenas o primeiro e segundo quadrante (olhando em sentido horário) com nossa curva. Vamos plotar nossos pontos e criar o gráfico utilizando o GeoGebra, mas você pode utilizar o software que preferir.
Passo 3
Plotando os pontos no software, e seguindo a tendencia dos pontos, temos o seguinte gráfico. Mas veja que caso queira maior precisão no traço do gráfico, basta aumentar a quantidade de pontos da sua tabela.
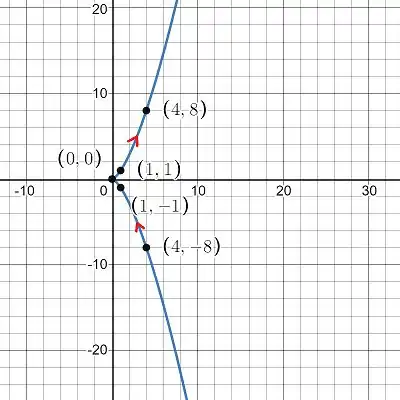
Podemos perceber que conforme cresce cresce junto.
Passo 4
Letra b)
Agora vamos voltar do mundo paramétrico para o cartesiano. A melhor solução para isso é isolar alguma das variáveis e substituir na outra.
Matematicamente será bem tranquilo, mas você vai precisar de uma intuição para qual a melhor variável para isolar seja ela ou . Vamos cair dentro então:
Desta vez não tem diferença qual dos lados isolamos. Vamos pegar então o
Substituindo em
Essa função não descreve tão bem assim nossa curva, porque tem uma limitação no domínio que não possui.
O mais certo seria dizer que
Bem, terminamos por aqui. Esses exercícios estão no início bem intuitivos, com o tempo vamos aprender mais ferramentas para construir gráficos. Te vejo na próxima resolução: )
