Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.6 - Ex. 18
18. Trace a cônica e sua diretriz. Também trace a curva obtida pela rotação dessa cônica ao redor de seu foco por um ângulo .
Passo 1
Eaee, belezinha?? Bom... o enunciado nos dá a seguinte equação de uma cônica:
Queremos esboçar essa cônica e calcular sua diretriz.
Para isso, vamos comparar a nossa equação com a seguinte equação geral:
Onde é a diretriz.
Com o valor da excentricidade, iremos identificar a cônica, onde:
- Se , trata-se de uma elipse;
- Se , trata-se de uma parábola;
- Se , trata-se de uma hipérbole.
Com a curva identificada, poderemos analisar e mostrar a equação da diretriz .
Em seguida, devemos plotar a curva obtida pela rotação dessa cônica ao redor de seu foco por um ângulo .
Agora bora lá!! 😉
Passo 2
Para começar vamos lembrar como é a equação polar, olha só:
Ele nos disse o seguinte:
Repare que o denominador é . Então vamos colocar o em evidência:
Então nossa equação fica:
Passo 3
Comparando com a equação da polar, temos:
Isolando eaplicando na primeira equação do sistema, encontramos a seguinte diretriz:
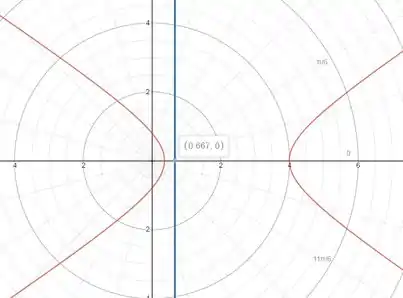
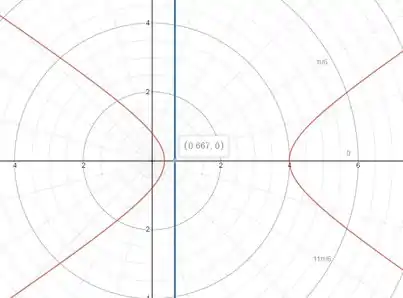
Como a excentricidade deu maior que , então nossa cônica é uma hipérbole.
Além disso, como teremos uma diretriz cuja equação é a seguinte:
Esboçando cônica, temos:
Passo 4
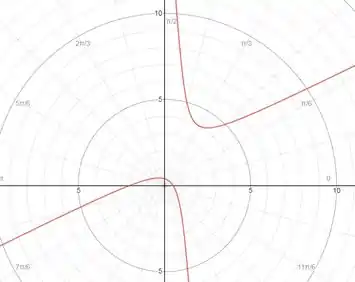
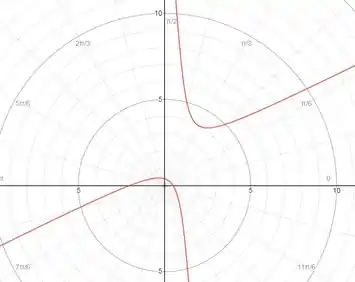
Quando rotacionarmos de um ângulo, teremos:
Para :
Esboçando o gráfico, temos:
Resposta
